第62页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
19.[答案含评分细则](2024江西赣州定南期末)(5分)如图,正方形ABCD内接于$\odot O$,M为$\overset{\frown}{AD}$上一点,且$\overset{\frown}{AM}=\overset{\frown}{DM}$,连接BM,CM,求证:$BM = CM$.(M9202002)


答案:
证明:
∵ 四边形 $ABCD$ 是正方形,
∴ $AB = CD$,
∴ $\overset{\frown}{AB}=\overset{\frown}{CD}$。 …… 2 分
∵ $\overset{\frown}{AM}=\overset{\frown}{DM}$,
∴ $\overset{\frown}{AB}+\overset{\frown}{AM}=\overset{\frown}{CD}+\overset{\frown}{DM}$, …… 4 分
即 $\overset{\frown}{BM}=\overset{\frown}{CM}$,
∴ $BM = CM$。 …… 5 分
∵ 四边形 $ABCD$ 是正方形,
∴ $AB = CD$,
∴ $\overset{\frown}{AB}=\overset{\frown}{CD}$。 …… 2 分
∵ $\overset{\frown}{AM}=\overset{\frown}{DM}$,
∴ $\overset{\frown}{AB}+\overset{\frown}{AM}=\overset{\frown}{CD}+\overset{\frown}{DM}$, …… 4 分
即 $\overset{\frown}{BM}=\overset{\frown}{CM}$,
∴ $BM = CM$。 …… 5 分
20.[答案含评分细则](2022山东青岛中考)(6分)已知二次函数$y = x^{2} + mx + m^{2} - 3$(m为常数,$m>0$)的图象经过点$P(2,4)$.(M9201004)
(1)求m的值.
(2)判断二次函数$y = x^{2} + mx + m^{2} - 3$的图象与x轴交点的个数,并说明理由.
(1)求m的值.
(2)判断二次函数$y = x^{2} + mx + m^{2} - 3$的图象与x轴交点的个数,并说明理由.
答案:
解析:
(1)将 $(2,4)$ 代入 $y = x^{2}+mx+m^{2}-3$,
得 $4 = 4+2m+m^{2}-3$,解得 $m_{1}=1$,$m_{2}=-3$, …… 2 分
∵ $m>0$,
∴ $m = 1$。…… 3 分
(2)二次函数 $y = x^{2}+mx+m^{2}-3$ 的图象与 $x$ 轴有 2 个交点。 …… 4 分
理由:
∵ $m = 1$,
∴ $y = x^{2}+x - 2$,
∴ $b^{2}-4ac = 1 + 8 = 9>0$,
∴ 二次函数的图象与 $x$ 轴有 2 个交点。 …… 6 分
(1)将 $(2,4)$ 代入 $y = x^{2}+mx+m^{2}-3$,
得 $4 = 4+2m+m^{2}-3$,解得 $m_{1}=1$,$m_{2}=-3$, …… 2 分
∵ $m>0$,
∴ $m = 1$。…… 3 分
(2)二次函数 $y = x^{2}+mx+m^{2}-3$ 的图象与 $x$ 轴有 2 个交点。 …… 4 分
理由:
∵ $m = 1$,
∴ $y = x^{2}+x - 2$,
∴ $b^{2}-4ac = 1 + 8 = 9>0$,
∴ 二次函数的图象与 $x$ 轴有 2 个交点。 …… 6 分
21.[答案含评分细则](2024山东济宁兖州模拟)(8分)已知$\triangle ABC$,请按以下要求完成本题.
(1)请作出$\triangle ABC$的外接圆$\odot O$(尺规作图,保留作图痕迹).
(2)若在$\triangle ABC$中,$\angle ABC = 65^{\circ}$,$\angle ACB = 45^{\circ}$,$\odot O$的直径AD交CB于E,求$\angle DEC$的度数.

(1)请作出$\triangle ABC$的外接圆$\odot O$(尺规作图,保留作图痕迹).
(2)若在$\triangle ABC$中,$\angle ABC = 65^{\circ}$,$\angle ACB = 45^{\circ}$,$\odot O$的直径AD交CB于E,求$\angle DEC$的度数.

答案:
解析:
(1)如图所示,$\odot O$ 即为所求。
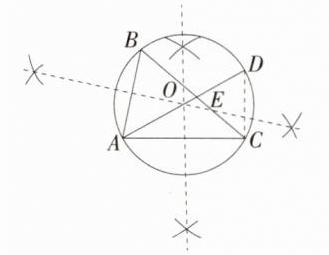
…… 4 分
(2)如图,连接 $CD$, …… 5 分
∵ $\overset{\frown}{AC}=\overset{\frown}{AC}$,
∴ $\angle ADC=\angle ABC = 65^{\circ}$。 …… 6 分
∵ $AD$ 为 $\odot O$ 的直径,
∴ $\angle ACD = 90^{\circ}$,
∴ $\angle DAC = 90^{\circ}-\angle ADC = 90^{\circ}-65^{\circ}=25^{\circ}$, …… 7 分
∴ $\angle DEC=\angle DAC+\angle ACB = 25^{\circ}+45^{\circ}=70^{\circ}$。…… 8 分
解析:
(1)如图所示,$\odot O$ 即为所求。

…… 4 分
(2)如图,连接 $CD$, …… 5 分
∵ $\overset{\frown}{AC}=\overset{\frown}{AC}$,
∴ $\angle ADC=\angle ABC = 65^{\circ}$。 …… 6 分
∵ $AD$ 为 $\odot O$ 的直径,
∴ $\angle ACD = 90^{\circ}$,
∴ $\angle DAC = 90^{\circ}-\angle ADC = 90^{\circ}-65^{\circ}=25^{\circ}$, …… 7 分
∴ $\angle DEC=\angle DAC+\angle ACB = 25^{\circ}+45^{\circ}=70^{\circ}$。…… 8 分
22.[答案含评分细则](2023北京中考)(8分)在平面直角坐标系$xOy$中,$M(x_{1},y_{1})$,$N(x_{2},y_{2})$是抛物线$y = ax^{2} + bx + c(a>0)$上的任意两点,设抛物线的对称轴为直线$x = t$.(M9201002)
(1)若对于$x_{1} = 1$,$x_{2} = 2$,有$y_{1} = y_{2}$,求t的值.
(2)若对于$0<x_{1}<1$,$1<x_{2}<2$,都有$y_{1}<y_{2}$,求t的取值范围.
(1)若对于$x_{1} = 1$,$x_{2} = 2$,有$y_{1} = y_{2}$,求t的值.
(2)若对于$0<x_{1}<1$,$1<x_{2}<2$,都有$y_{1}<y_{2}$,求t的取值范围.
答案:
解析:
(1)
∵ 对于 $x_{1}=1$,$x_{2}=2$,有 $y_{1}=y_{2}$,
∴ 抛物线的对称轴为直线 $x=\frac{x_{1}+x_{2}}{2}=\frac{3}{2}$,
∴ $t=\frac{3}{2}$。 …… 4 分
(2)
∵ $0<x_{1}<1$,$1<x_{2}<2$,
∴ $\frac{1}{2}<\frac{x_{1}+x_{2}}{2}<\frac{3}{2}$,$x_{1}<x_{2}$。 …… 6 分
∵ $y_{1}<y_{2}$,$a>0$,
∴ 点 $M(x_{1},y_{1})$ 离抛物线的对称轴(直线 $x = t$)更近,
∴ 线段 $MN$ 的中点在对称轴的右侧,
即 $\frac{x_{1}+x_{2}}{2}>t$,
∴ $t\leq\frac{1}{2}$。 …… 8 分
(1)
∵ 对于 $x_{1}=1$,$x_{2}=2$,有 $y_{1}=y_{2}$,
∴ 抛物线的对称轴为直线 $x=\frac{x_{1}+x_{2}}{2}=\frac{3}{2}$,
∴ $t=\frac{3}{2}$。 …… 4 分
(2)
∵ $0<x_{1}<1$,$1<x_{2}<2$,
∴ $\frac{1}{2}<\frac{x_{1}+x_{2}}{2}<\frac{3}{2}$,$x_{1}<x_{2}$。 …… 6 分
∵ $y_{1}<y_{2}$,$a>0$,
∴ 点 $M(x_{1},y_{1})$ 离抛物线的对称轴(直线 $x = t$)更近,
∴ 线段 $MN$ 的中点在对称轴的右侧,
即 $\frac{x_{1}+x_{2}}{2}>t$,
∴ $t\leq\frac{1}{2}$。 …… 8 分
23.[答案含评分细则](2023湖南郴州中考)(9分)如图,在$\odot O$中,AB是直径,点C是圆上一点.在AB的延长线上取一点D,连接CD,CB,$\angle BCD = \angle A$.(M9202005)
(1)求证:直线CD是$\odot O$的切线.
(2)若$\angle ACD = 120^{\circ}$,$CD = 2\sqrt{3}$,求图中阴影部分的面积(结果用含$\pi$的式子表示).
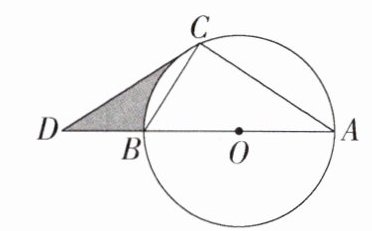
(1)求证:直线CD是$\odot O$的切线.
(2)若$\angle ACD = 120^{\circ}$,$CD = 2\sqrt{3}$,求图中阴影部分的面积(结果用含$\pi$的式子表示).

答案:
解析:
(1)证明:连接 $OC$, …… 1 分
∵ $AB$ 是 $\odot O$ 的直径,
∴ $\angle ACB=\angle OCA+\angle OCB = 90^{\circ}$, …… 2 分
∵ $OA = OC$,$\angle BCD=\angle A$,
∴ $\angle OCA=\angle A=\angle BCD$,
∴ $\angle OCD=\angle BCD+\angle OCB = 90^{\circ}$,
∴ $OC\perp CD$,
∴ 直线 $CD$ 是 $\odot O$ 的切线。 …… 4 分
(2)
∵ $\angle ACD = 120^{\circ}$,$\angle ACB = 90^{\circ}$,
∴ $\angle A=\angle BCD = 120^{\circ}-90^{\circ}=30^{\circ}$,
∴ $\angle BOC = 2\angle A = 60^{\circ}$。 …… 5 分
在 $Rt\triangle OCD$ 中,$\tan\angle BOC=\frac{CD}{OC}=\tan60^{\circ}$,$CD = 2\sqrt{3}$,
∴ $OC=\frac{CD}{\tan60^{\circ}}=\frac{2\sqrt{3}}{\sqrt{3}}=2$, …… 7 分
∴ $S_{阴影}=S_{\triangle COD}-S_{扇形 BOC}=\frac{1}{2}\times2\sqrt{3}\times2-\frac{60\pi\times2^{2}}{360}$
$=2\sqrt{3}-\frac{2\pi}{3}$。 …… 9 分
(1)证明:连接 $OC$, …… 1 分
∵ $AB$ 是 $\odot O$ 的直径,
∴ $\angle ACB=\angle OCA+\angle OCB = 90^{\circ}$, …… 2 分
∵ $OA = OC$,$\angle BCD=\angle A$,
∴ $\angle OCA=\angle A=\angle BCD$,
∴ $\angle OCD=\angle BCD+\angle OCB = 90^{\circ}$,
∴ $OC\perp CD$,
∴ 直线 $CD$ 是 $\odot O$ 的切线。 …… 4 分
(2)
∵ $\angle ACD = 120^{\circ}$,$\angle ACB = 90^{\circ}$,
∴ $\angle A=\angle BCD = 120^{\circ}-90^{\circ}=30^{\circ}$,
∴ $\angle BOC = 2\angle A = 60^{\circ}$。 …… 5 分
在 $Rt\triangle OCD$ 中,$\tan\angle BOC=\frac{CD}{OC}=\tan60^{\circ}$,$CD = 2\sqrt{3}$,
∴ $OC=\frac{CD}{\tan60^{\circ}}=\frac{2\sqrt{3}}{\sqrt{3}}=2$, …… 7 分
∴ $S_{阴影}=S_{\triangle COD}-S_{扇形 BOC}=\frac{1}{2}\times2\sqrt{3}\times2-\frac{60\pi\times2^{2}}{360}$
$=2\sqrt{3}-\frac{2\pi}{3}$。 …… 9 分
查看更多完整答案,请扫码查看


