《2025年5年中考3年模拟九年级数学下册湘教版》

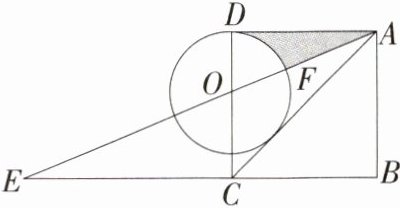
23.(2024湖南怀化溆浦一模)(8分)如图,点E是正方形ABCD的边BC的延长线上一点,且AC = CE,连接AE交CD于点O,以点O为圆心,OD的长为半径作☉O,☉O交线段AO于点F.
(1)求证:AC是☉O的切线.
(2)若AB = 2$\sqrt{2}$+2,求阴影部分的面积.

答案：
解析
(1)证明：如图，过O作$OH⊥AC$于点H，
∵四边形ABCD是正方形，
∴$∠ADO = 90^{\circ}$，$AD// BE$，
∴$∠DAO = ∠E$.
∵$AC = CE$，
∴$∠E = ∠CAO$，
∴$∠DAO = ∠CAO$，
∴$OD = OH$，即OH为$⊙O$的半径，
∴AC是$⊙O$的切线.

(2)
∵四边形ABCD是正方形，
∴$∠ACD = ∠DAH = 45^{\circ}$，
∴$\triangle COH$是等腰直角三角形，
∴$OC=\sqrt{2}OH=\sqrt{2}OD$.
∵$DC = AB = 2\sqrt{2}+2$，
∴$OD+\sqrt{2}OD = 2\sqrt{2}+2$，
∴$OD = 2$，
∵$∠DAO = ∠HAO=\frac{1}{2}∠DAH = 22.5^{\circ}$，
∴$∠AOD = 90^{\circ}-22.5^{\circ}=67.5^{\circ}$，
∴$S_{阴影}=S_{Rt\triangle ADO}-S_{扇形DOF}=\frac{1}{2}\times(2\sqrt{2}+2)\times2-\frac{67.5\pi\times2^{2}}{360}=2\sqrt{2}+2-\frac{3\pi}{4}$.

24. [新考向·实践探究试题] (2024湖南中考)(10分)
【问题背景】
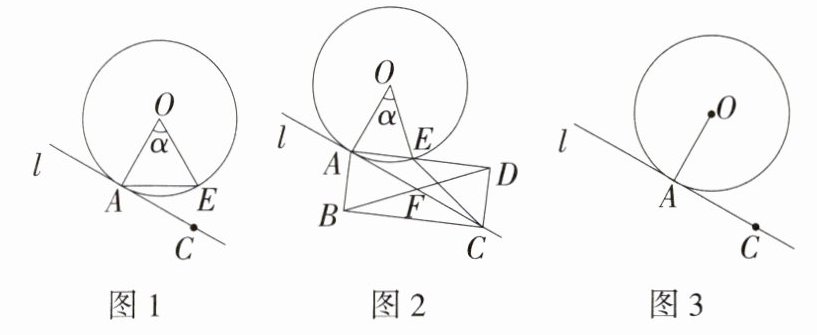
已知点A是半径为r的☉O上的定点,连接OA,将线段OA绕点O按逆时针方向旋转α(0°＜α＜90°)得到OE,连接AE,过点A作☉O的切线l,在直线l上取点C,使得∠CAE为锐角.(M9202005)

【初步感知】
(1)如图1,当α = 60°时,∠CAE = ________°.
【问题探究】
(2)以线段AC为对角线作矩形ABCD,使得边AD过点E,连接CE,对角线AC,BD相交于点F.
①如图2,当AC = 2r时,求证:无论α在给定的范围内如何变化,BC = CD + ED总成立.
②如图3,当AC = $\frac{4}{3}$r,$\frac{CE}{OE}=\frac{2}{3}$时,请补全图形,并求tan α及$\frac{AB}{BC}$的值.

答案：
解析
(1)
∵$∠AOE=\alpha = 60^{\circ}$，$OA = OE$，
∴$\triangle AOE$是等边三角形，
∴$∠OAE = ∠OEA = 60^{\circ}$，
∵AC与$⊙O$相切，
∴$∠OAC = 90^{\circ}$，
∴$∠CAE = 90^{\circ}-60^{\circ}=30^{\circ}$.
(2)①证明：
∵四边形ABCD是矩形，$AC = 2r$，
∴$CF = DF = r = OA = OE$，
∵$∠OAC = ∠ADC = 90^{\circ}$，
∴$∠OAE + ∠CAD = ∠ACD + ∠CAD = 90^{\circ}$，
∴$∠OAE = ∠ACD$.
∵$OA = OE$，$CF = DF$，
∴$∠OEA = ∠OAE = ∠FCD = ∠FDC$，
∴$\triangle OAE≌\triangle FCD$，
∴$AE = CD$.
∵$BC = AD = AE + ED$，
∴$BC = CD + ED$，此结论与$\alpha$的值无关，
∴无论$\alpha$在给定的范围内如何变化，$BC = CD + ED$总成立.
②补全图形如图，连接OC，

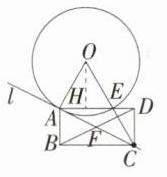
∵AC是$⊙O$的切线，
∴$∠OAC = 90^{\circ}$.
∵$AC=\frac{4}{3}r$，
∴$\tan\alpha=\frac{AC}{OA}=\frac{4}{3}$.设$OA = 3m$，则$AC = 4m$，
∴$OC = 5m$.
∵$\frac{CE}{OE}=\frac{2}{3}$，$OE = OA = 3m$，
∴$CE = 2m$，
∴$OE + CE = 5m = OC$，即点E在线段OC上.如图，过O点作$OH⊥AE$于H，则$AH = EH$，
∵$∠OHE = 90^{\circ}=∠D$，$∠OEH = ∠CED$，
∴$\triangle OEH\sim\triangle CED$，
∴$\frac{EH}{ED}=\frac{OE}{CE}=\frac{3}{2}$.设$EH = AH = 3a$，则$DE = 2a$，
∴$AD = AH + EH + ED = 8a$，在$Rt\triangle ACD$中，$CD^{2}=AC^{2}-AD^{2}=16m^{2}-64a^{2}$，在$Rt\triangle CED$中，$CD^{2}=CE^{2}-ED^{2}=4m^{2}-4a^{2}$，
∴$16m^{2}-64a^{2}=4m^{2}-4a^{2}$，解得$a=\frac{\sqrt{5}}{5}m$，
∴$BC = AD = 8a=\frac{8\sqrt{5}}{5}m$，$AB = CD=\sqrt{4m^{2}-4a^{2}}=\frac{4\sqrt{5}}{5}m$，
∴$\frac{AB}{BC}=\frac{\frac{4\sqrt{5}}{5}m}{\frac{8\sqrt{5}}{5}m}=\frac{1}{2}$.