《2025年5年中考3年模拟九年级数学下册湘教版》

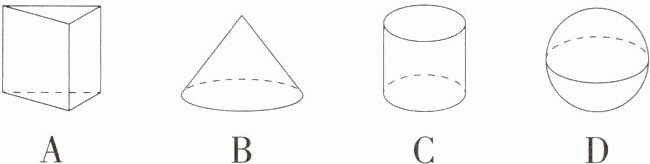
1.（2023 湖南郴州中考）下列几何体中，各自的三视图完全一样的是(M9203003) （ ）

答案： D     A. 三棱柱的主视图和左视图的轮廓是矩形，俯视图是三角形，故本选项不合题意；B. 圆锥的主视图和左视图是等腰三角形，俯视图是带圆心的圆，故本选项不合题意；C. 圆柱的主视图和左视图是矩形，俯视图是圆，故本选项不合题意；D. 球的主视图、左视图、俯视图是全等的圆，故本选项符合题意. 故选 D.

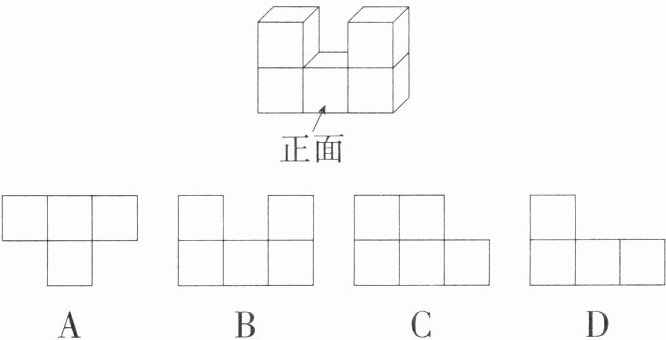
2.（2022 湖南长沙中考）如图所示的是由5个大小相同的小正方体组成的几何体，则该几何体的主视图是(M9203003) （ ）

答案： B   该几何体的主视图有 3 列，从左向右，第 1 列有 2 个小正方形，第 2 列有 1 个小正方形，第 3 列有 2 个小正方形. 故选 B.

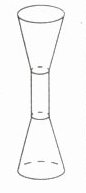
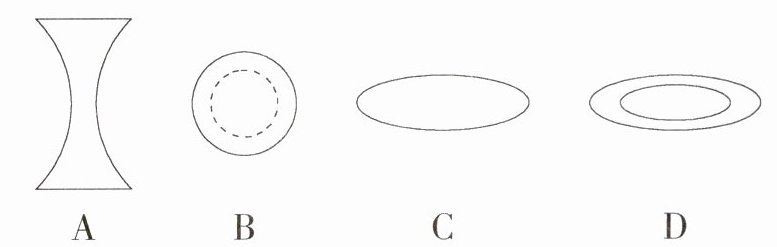
3. 湖南传统舞蹈·长鼓舞（2022 湖南永州中考）永州市江华县有“神州瑶都”的美称，每逢“盘王节”会表演长鼓舞，长鼓舞中使用的“长鼓”内腔挖空，两端相通，两端鼓口为圆形，中间鼓腰较为细小.如图所示的是类似“长鼓”的几何体，其俯视图的大致形状是(M9203003) （ ）

答案： B    由题意可知，该几何体的俯视图为圆形，且中间有一个小一些的虚线圆. 故选 B.

4. 情境题·数学文化（2024 湖南株洲芦淞模拟）我国古代数学名著《九章算术》中，将底面是直角三角形的直三棱柱称之为“堑堵”.堑堵的实物图与左视图如图所示，根据图中的数据可得该“堑堵”的高h为________.(M9203004)

答案：   4
解析
∵ 该“堑堵”的左视图是直角三角形，且高 h 所在的直角边对应的角为 30°，
∴ 该“堑堵”的高 h = $\frac{1}{2}$×8 = 4.

5.（教材变式·P108T2）(2024 山东济宁高新区期末）如图所示的是由两个长方体组成的几何体，这两个长方体的底面都是正方形，画出这个几何体的主视图、左视图和俯视图.(M9203003)

答案：
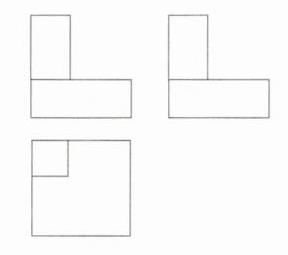
解析 如图所示：

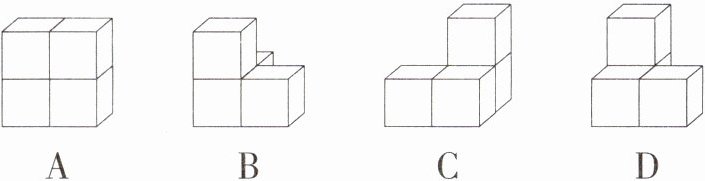
6.（2024 山东威海中考,5,★★☆）下列几何体都是由四个大小相同的小正方体搭成的.其中主视图、左视图和俯视图完全相同的是(M9203003) （ ）

答案： D   A. 三个视图均不相同，主视图的下面是两个正方形，上面是两个正方形，左视图是一列两个正方形，俯视图是一行两个正方形，不合题意. B. 主视图和俯视图相同，下面是两个正方形，上面的左边是一个正方形，左视图的下面是两个正方形，上面的右边是一个正方形，不合题意. C. 主视图和俯视图相同，下面是两个正方形，上面的右边是一个正方形，左视图的下面是两个正方形，上面的左边是一个正方形，不合题意. D. 三个视图相同，下面是两个正方形，上面的左边是一个正方形，符合题意. 故选 D.

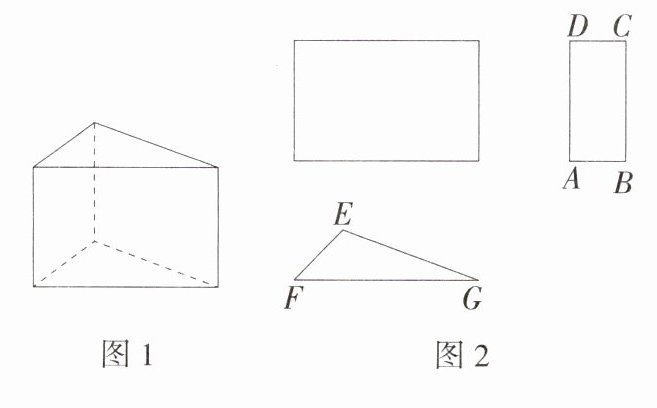
7.（2024 湖南长沙岳麓麓山外国语实验中学月考,18,★★☆）某直三棱柱零件如图1所示，张师傅根据此零件按1：1的比例画出准确的三视图（如图2）.已知在△EFG中，EF = 4 cm，∠EFG = 45°，FG = 12 cm，在左视图中，AD = 8 cm.求：
（1）AB的长.
（2）这个直三棱柱的体积.

答案： 解析
(1) 在△EFG 中，过点 E 作 EH⊥FG 于点 H. 在 Rt△EHF 中，EF = 4 cm，∠EFH = 45°，
∴ ∠FEH = ∠EFH = 45°，
∴ FH = EH = $\frac{\sqrt{2}}{2}$EF = $\frac{\sqrt{2}}{2}$×4 = 2$\sqrt{2}$(cm)，
∴ AB = EH = 2$\sqrt{2}$ cm.
(2) $V_{直三棱柱}$ = $S_{\triangle EFG}$·AD = $\frac{1}{2}$×12×2$\sqrt{2}$×8 = 96$\sqrt{2}$(cm³).