《2025年5年中考3年模拟九年级数学下册湘教版》

8.（2024 湖南长沙天心湘郡培粹中学月考）如图，抛物线$y = ax^{2}$与直线$y = bx + c$的两个交点分别为$A(-3,9),B(1,1)$，则关于$x$的方程$ax^{2}-bx - c = 0$的解为__________.(M9201004)

答案： $x_{1}=-3,x_{2}=1$
解析：由题中图象可知，关于$x$的方程$ax^{2}-bx - c = 0$的解就是抛物线$y = ax^{2}$与直线$y = bx + c$的两个交点$A(-3,9),B(1,1)$的横坐标，故$x_{1}=-3,x_{2}=1$.

9.（2023 湖南长沙明德教育集团期中）如图，抛物线$y = ax^{2}+bx + c$的对称轴是直线$x = -2$，抛物线与$x$轴的一个交点在点$(-4,0)$和点$(-3,0)$之间，下列结论中正确的有（ ）
①$4a - b = 0$；②$4a\lt c$；③关于$x$的方程$ax^{2}+bx + c - 3 = 0$有两个相等的实数根；④$b^{2}+2b\gt4ac$.

A.1个
B.2个
C.3个
D.4个

答案： D：$\because$抛物线的对称轴为直线$x=-\frac{b}{2a}=-2$，$\therefore 4a - b = 0$，故①正确.$\because$抛物线与$x$轴的一个交点在点$(-3,0)$和$(-4,0)$之间，对称轴为直线$x = - 2$，$\therefore$抛物线与$x$轴的另一个交点在点$(-1,0)$和$(0,0)$之间，$\therefore x = - 1$时，$y＞0$，即$a + b + c＞0$，又$\because b = 4a$，$\therefore a - b + c=a - 4a + c=-3a + c＞0$，$\therefore 3a＜c$，$\because a＜0$，$\therefore 4a＜c$，故②正确.$\because$抛物线的顶点坐标为$(-2,3)$，$\therefore$抛物线与直线$y = 3$有一个交点，$\therefore$关于$x$的方程$ax^{2}+bx + c = 3$，即$ax^{2}+bx + c - 3 = 0$有两个相等的实数根，故③正确.$\because$抛物线的顶点坐标为$(-2,3)$，$\therefore\frac{4ac - b^{2}}{4a}＞2$，又$\because a＜0$，$\therefore 4ac - b^{2}＜8a$，$\because b = 4a$，$\therefore 4ac - b^{2}＜2b$，$\therefore b^{2}+2b＞4ac$，故④正确. 故选 D.

10. 一线三等角模型（2023 湖南长沙三模）如图，$AB\perp BC$于点$B$，$DC\perp BC$于点$C$，点$E$是线段$BC$上一个动点，$AE\perp EF$于点$E$，射线$EF$交射线$CD$于点$F$，$BC = 2AB = 8$，设$BE = x$，$CF = y$，当点$E$从点$B$运动到点$C$时，$y$与$x$的函数图象大致是（ ）

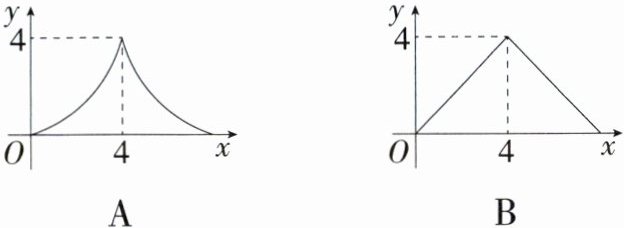
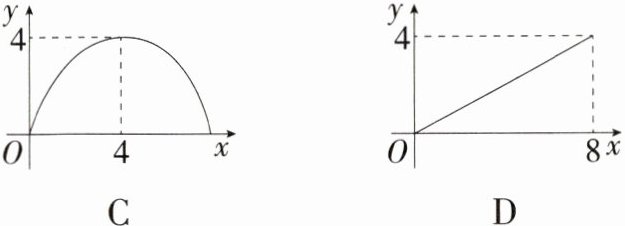
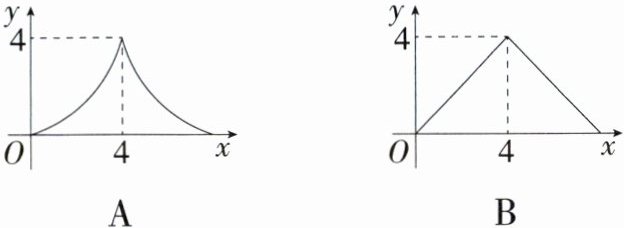
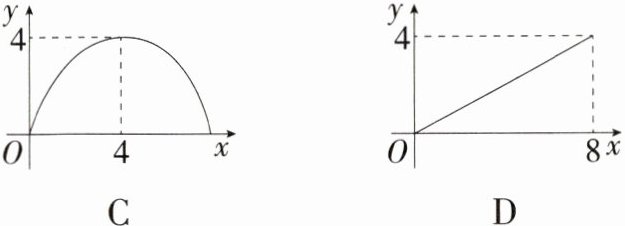
答案： C：$\because AE\perp EF$，$\therefore\angle AEB+\angle FEC = 90^{\circ}$，$\because AB\perp BC$，$DC\perp BC$，$\therefore\angle B=\angle C = 90^{\circ}$，$\therefore\angle BAE+\angle AEB = 90^{\circ}$，$\therefore\angle BAE=\angle FEC$，$\therefore\triangle ABE\backsim\triangle ECF$，$\therefore\frac{AB}{EC}=\frac{BE}{FC}$.
$\because BC = 2AB = 8$，$BE = x$，$\therefore AB = 4$，$EC = 8 - x$，$\therefore\frac{4}{8 - x}=\frac{x}{y}$，$\therefore y=-\frac{1}{4}x^{2}+2x=-\frac{1}{4}(x - 4)^{2}+4$，$\therefore y$关于$x$的函数图象为抛物线，抛物线开口向下，顶点坐标为$(4,4)$. 故选 C.

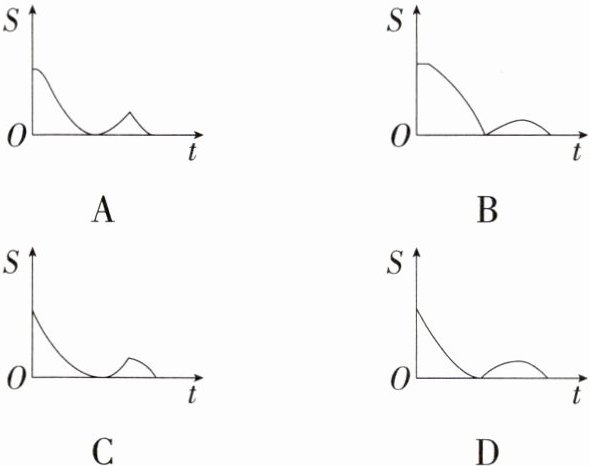
11.（2024 湖南岳阳二模）如图，在矩形$ABCD$中，$BC = 1$，$\angle ADB = 60^{\circ}$，动点$P$沿路线$AD→DB$运动到点$B$，同时动点$Q$沿路线$DB→BC$运动到点$C$，点$P,Q$在矩形边上的运动速度为每秒 1 个单位长度，在矩形对角线上的运动速度为每秒 2 个单位长度.设运动时间为$t$秒，$\triangle PBQ$的面积为$S$，则下列图象能大致反映$S$与$t$之间函数关系的是（$\triangle PBQ$不存在时默认面积为 0）（ ）

答案： D：$\because$四边形$ABCD$是矩形，$\therefore AD = BC = 1$，$\angle A=\angle ADC=\angle C = 90^{\circ}$，$\because\angle ADB = 60^{\circ}$，$\therefore\angle CDB = 30^{\circ}$，$\therefore BD = 2BC = 2$，当点$P$在$AD$上时，$S=\frac{1}{2}\times BQ\times BQ$上的高$=\frac{1}{2}(2 - 2t)\cdot(1 - t)\cdot\sin60^{\circ}=\frac{\sqrt{3}}{2}(1 - t)^{2}(0＜t＜1)$. 当点$P$在线段$BD$上时，$S=\frac{1}{2}\times BP\times BP$上的高$=\frac{1}{2}[2 - 2(t - 1)]\cdot\frac{\sqrt{3}}{2}(t - 1)=-\frac{\sqrt{3}}{2}t^{2}+\frac{3\sqrt{3}}{2}t-\sqrt{3}(1＜t\leqslant2)$. 只有 D 选项中的图象符合.
观察选项可知，选项 D 满足条件，故选 D.

12.（2023 湖南长沙浏阳一模）如图 1，点$P$从$\triangle ABC$的顶点$B$出发，沿$B→C→A$匀速运动到点$A$，图 2 是点$P$运动时，线段$BP$的长度$y$随时间$x$变化的关系图象，其中$M$是曲线部分的最低点，则$\triangle ABC$的面积是（ ）
        
A.12
B.24
C.36
D.48

答案： D：由题图 2 知，$AB = BC = 10$，当$BP\perp AC$时，$y$的值最小，为 8，即$\triangle ABC$中，$AC$边上的高为 8. 当$y = 8$时，$PC=\sqrt{10^{2}-8^{2}}=6$，$\therefore AC = 12$，$\therefore S_{\triangle ABC}=\frac{1}{2}\times12\times8 = 48$，故选 D.