《2025年5年中考3年模拟九年级数学下册湘教版》

9.(2022湖南岳阳中考)已知二次函数$y = mx^{2} - 4m^{2}x - 3$(m为常数，$m\neq0$)，点$P(x_{P},y_{P})$是该函数图象上的一点，当$0\leqslant x_{P}\leqslant4$时，$y_{P}\leqslant - 3$，则m的取值范围是 ( )
A.$m\geqslant1$或$m＜0$
B.$m\geqslant1$
C.$m\leqslant - 1$或$m＞0$
D.$m\leqslant - 1$

答案： A：二次函数 $y = mx^{2}-4m^{2}x - 3$ 的图象的对称轴为直线 $x = 2m$，与 $y$ 轴的交点坐标为 $(0,-3)$。①当 $m＞0$ 时，$2m＞0$，对称轴在 $y$ 轴右侧，此时，当 $x = 4$ 时，$y\leq -3$，即 $4^{2}m-4m^{2}\times4 - 3\leq -3$，解得 $m\geq 1$ 或 $m\leq 0$，
∵ $m＞0$，
∴ $m\geq 1$。②当 $m＜0$ 时，$2m＜0$，对称轴在 $y$ 轴左侧，当 $0\leq x\leq 4$ 时，$y$ 随 $x$ 的增大而减小，故当 $0\leq x_{p}\leq 4$ 时，$y_{p}\leq -3$ 恒成立。综上，$m$ 的取值范围是 $m\geq 1$ 或 $m＜0$。故选 A。

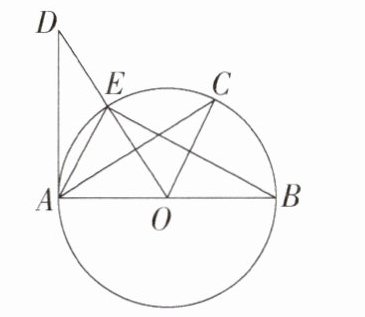
10.(2023湖南长沙一模)如图，已知AB是$\odot O$的直径，DA与$\odot O$相切于点A，OD与$\odot O$相交于点E，C是弧BE的中点，现有如下几个结论：①$BA\perp DA$；②$OC// AE$；③$\angle COE = 2\angle CAE$；④$\angle B = \angle BAC$，其中正确的有 ( )


A.1个
B.2个
C.3个
D.4个

答案： C：
∵ $AB$ 是 $\odot O$ 的直径，$DA$ 与 $\odot O$ 相切于点 $A$，
∴ $AB\perp DA$，故 ① 正确；
∵ $C$ 是弧 $BE$ 的中点，
∴ $\angle COE=\angle COB$，$\angle CAE=\angle BAC$，
∵ $OE = OB$，
∴ $OC\perp BE$，
∵ $AB$ 是 $\odot O$ 的直径，
∴ $AE\perp BE$，
∴ $OC// AE$，故②正确；
∵ $\angle COE$ 是 $\overset{\frown}{CE}$ 所对的圆心角，$\angle CAE$ 是 $\overset{\frown}{CE}$ 所对的圆周角，
∴ $\angle COE = 2\angle CAE$，故③正确；当 $\angle B=\angle BAC$ 时，
∵ $\angle CAE=\angle BAC$，$\angle AEB = 90^{\circ}$，
∴ $\angle CAE+\angle BAC+\angle B = 3\angle B = 90^{\circ}$，
∴ $\angle B = 30^{\circ}$，但 $\angle B$ 不一定等于 $30^{\circ}$，
∴ $\angle B$ 不一定等于 $\angle BAC$，故④错误。
∴ 正确的结论是①②③，共 3 个。故选 C。

11. 新独家原创 有下列说法：①弧分为优弧和劣弧两种；②圆是轴对称图形，任意一条直径都是它的对称轴；③三点确定一个圆；④中心角是$45^{\circ}$的正多边形是中心对称图形.其中正确的是________.(填序号)

答案：  ④
解析：弧分为优弧、劣弧和半圆三种，故①说法错误。圆是轴对称图形，任意一条直径所在的直线都是它的对称轴，故②说法错误。不在同一直线上的三点确定一个圆，故③说法错误。中心角是 $45^{\circ}$ 的正多边形是正八边形，是中心对称图形，故④说法正确。

12. 新独家原创 将抛物线$y = ax^{a - 1}$向左平移a个单位长度，所得的新抛物线的顶点坐标为________.(M9201002)

答案：  $(-3,0)$
解析：
∵ 函数 $y = ax^{a - 1}$ 的图象是抛物线，
∴ $a - 1 = 2$，解得 $a = 3$，
∴ 原抛物线的表达式为 $y = 3x^{2}$，则新抛物线的表达式为 $y = 3(x + 3)^{2}$，其顶点坐标为 $(-3,0)$。

13.(2024江苏扬州广陵期中)已知$\triangle ABC$的面积是$54\ cm^{2}$，周长是36 cm，则$\triangle ABC$的内切圆的半径是________cm.(M9202004)

答案：  3
解析：设 $\triangle ABC$ 的内切圆半径为 $r\ cm$，则 $\frac{1}{2}r\times36 = 54$，解得 $r = 3$，即 $\triangle ABC$ 的内切圆的半径是 $3\ cm$。

14.(2023湖南长沙郡教育集团模拟)如图，直线PA、PB、MN分别与$\odot O$相切于点A、B、D，$PA = PB = 4\ cm$，则$\triangle PMN$的周长是________.

答案：  $8\ cm$
解析：
∵ 直线 $PA$、$PB$、$MN$ 分别与 $\odot O$ 相切于点 $A$、$B$、$D$，
∴ $MA = MD$，$ND = NB$，
∴ $\triangle PMN$ 的周长 $= PM + PN+MD + ND = PM + MA + PN + NB = PA + PB = 4 + 4 = 8(cm)$。

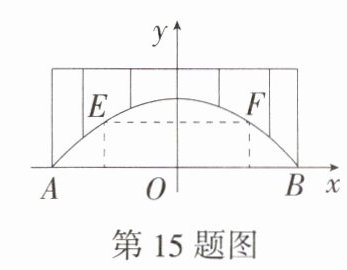
15.(2024湖南娄底新化一模)“廊桥”是我国古代劳动人民实践和智慧的结晶，具有极高的科学、文化、历史、艺术价值.如图所示的是某座抛物线形廊桥的示意图，已知抛物线的函数表达式为$y = -\frac{2}{81}x^{2} + 10$，为保护廊桥的安全，在该抛物线型廊桥上距水面(AB)8米的点E，F处安装两盏警示灯，则这两盏警示灯的水平距离EF是________米.

答案：  18
解析：由题意可知点 $E$，$F$ 的纵坐标均为 8，把 $y = 8$ 代入函数 $y = -\frac{2}{81}x^{2}+10$，得 $8 = -\frac{2}{81}x^{2}+10$，解得 $x=\pm9$，
∴ 点 $E$，$F$ 的横坐标分别为 $-9$，$9$，
∴ $EF = 9-(-9)=18$（米）。

16. 湖南特产·醴陵瓷碗(2024湖南长沙模拟)“天下名瓷出醴陵”，湖南省醴陵是釉下五彩瓷的原产地，生产的瓷器闻名四方.醴陵生产的某种瓷碗的正面形状示意图如图所示，$\overset{\frown}{AB}$是$\odot O$的一部分，D是$\overset{\frown}{AB}$的中点，连接OD，与弦AB交于点C，连接$OA$，$OB$.已知$AB = 24\ cm$，碗深$CD = 8\ cm$，则$\odot O$的半径$OA$为________cm.

答案：  13
解析：由题意可知半径 $OD\perp AB$，
∴ $AC = BC=\frac{1}{2}AB = 12\ cm$，设半径 $OA = r\ cm$，则 $OC=(r - 8)\ cm$。在 $Rt\triangle AOC$ 中，$OC^{2}+AC^{2}=OA^{2}$，
∴ $(r - 8)^{2}+12^{2}=r^{2}$，解得 $r = 13$，即 $\odot O$ 的半径 $OA$ 为 $13\ cm$。

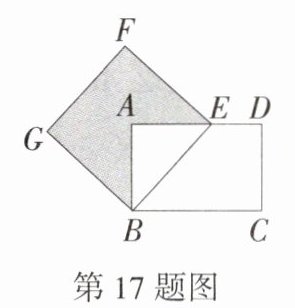
17.(2024陕西西安阎良期末)如图，在矩形ABCD中，$AB = 2$，$AD = 3$，动点E从点D出发沿DA向终点A运动，连接BE，以BE为边在BE上方作正方形BEFG，在点E运动的过程中，图中阴影部分的面积最小为________.

答案： $\frac{15}{4}$
解析：设 $AE = x$，则正方形 $BEFG$ 的面积 $= BE^{2}=AE^{2}+AB^{2}=x^{2}+2^{2}=x^{2}+4$，
∵ $\triangle ABE$ 的面积为 $\frac{1}{2}\times2x = x$，
∴ $S_{阴影}=x^{2}+4 - x=(x-\frac{1}{2})^{2}+\frac{15}{4}$，
∴ 当 $x=\frac{1}{2}$ 时，阴影部分的面积最小，最小值为 $\frac{15}{4}$。

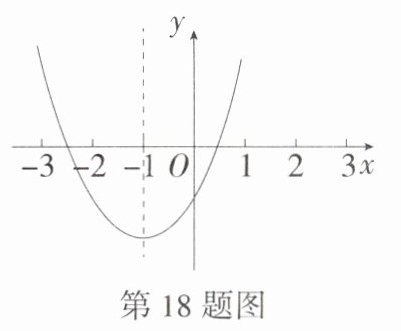
18.(2024湖南郴州汝城期末)已知二次函数$y = ax^{2} + bx + c$的图象如图，其对称轴为直线$x = - 1$，给出下列结论：①$b^{2}＞4ac$；②$abc＞0$；③$2a + b = 0$；④$a - b + c＜0$；⑤$3a + c＞0$.其中正确结论的序号是________.(M9201003)

答案：  ①④⑤
解析：
∵ 函数图象和 $x$ 轴有两个交点，
∴ $b^{2}-4ac＞0$，
∴ $b^{2}＞4ac$，结论①正确。由图象可知 $a＞0$，$c＜0$，$-\frac{b}{2a}=-1$，
∴ $b = 2a＞0$，
∴ $abc＜0$，结论②错误。
∵ $b = 2a＞0$，
∴ $2a + b = 4a＞0$，结论③错误。
∵ $x = -1$ 时，$y＜0$，
∴ $a - b + c＜0$，结论④正确。
∵ $x = 1$ 时，$y＞0$，
∴ $a + b + c＞0$，又
∵ $b = 2a$，
∴ $3a + c＞0$，结论⑤正确。综上可知，正确结论的序号是①④⑤。