《2025年5年中考3年模拟九年级数学下册湘教版》

1.(2023湖南永州中考改编)下列几何体的三视图中，主视图和左视图都为三角形的是(M9203003) ( )

答案： A. 主视图和左视图都为矩形，不合题意；B. 主视图和左视图都为正方形，不合题意；C. 主视图和左视图都为矩形，不合题意；D. 主视图和左视图都为等腰三角形，符合题意. 故选 D.

2.(2024江苏宿迁沭阳联考)△ABC的外心在三角形的一边上，则△ABC是 ( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.无法判断

答案： B  锐角三角形的外心在三角形的内部，直角三角形的外心是其斜边的中点，钝角三角形的外心在三角形的外部. 由此可知若三角形的外心在三角形的一条边上，则这个三角形是直角三角形. 故选 B.

3.(2023湖南长沙雨花期末)关于频率与概率有下列几种说法，其中正确的是(M9204001) ( )
①“明天下雨的概率是90%”表示明天下雨的可能性很大；
②“抛一枚质地均匀的硬币，正面朝上的概率为0.5”表示每抛两次就有一次正面朝上；
③“某彩票中奖的概率是1%”表示买10张该种彩票不可能中奖；
④“抛一枚质地均匀的硬币，正面朝上的概率为0.5”表示随着抛掷次数的增加，“正面朝上”这一事件发生的频率稳定在0.5左右.
A.①③
B.①④
C.②③
D.②④

答案： B   ①“明天下雨的概率是 90%”表示明天下雨的可能性很大，此说法正确；②“抛一枚质地均匀的硬币，正面朝上的概率为 0.5”表示平均每抛两次就有一次正面朝上，原说法错误；③“某彩票中奖的概率是 1%”表示平均每买 100 张该种彩票有一次中奖，原说法错误；④“抛一枚硬币正面朝上的概率为 0.5”表示随着抛掷次数的增加，“正面朝上”这一事件发生的频率稳定在 0.5 左右，此说法正确. 故选 B.

4.跨语文·《诫子书》(2024湖南邵阳邵东三模)“非学无以广才”，意为不学习就难以增长才干，出自诸葛亮的《诫子书》.将“非学无以广才”六个字分别写在一个正方体的六个面上，展开图如图所示，那么该正方体中和“学”字所在面相对的面上的字是(M9203002) ( )


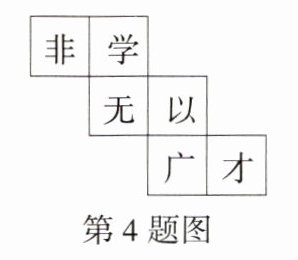
A.无
B.以
C.广
D.才

答案： C  把展开图折叠成正方体，可知“非”和“以”相对，“学”和“广”相对，“无”和“才”相对. 故选 C.

5.情境题·中华优秀传统文化(2024湖南十三市州模拟)八卦图是中国古老的科学文化遗产，是我国古代劳动人民智慧的结晶，古人认为，世间万物皆可分类归至八卦之中.相传，德国数学家莱布尼茨受八卦图的启发而发明了电子计算机使用的二进制.八卦图中的每一卦由三根线组成.如果从图中任选一卦，那么这一卦中恰有2根“”和1根“”的概率是 ( )

A.$\frac{1}{8}$
B.$\frac{1}{2}$
C.$\frac{3}{8}$
D.$\frac{5}{8}$

答案： C  从八卦图中任取一卦，共有 8 种等可能的结果，其中卦中恰有 2 根“——”和 1 根“— —”的结果有 3 种，
∴ 这一卦中恰有 2 根“——”和 1 根“— —”的概率为$\frac{3}{8}$. 故选 C.

6.(2024广东珠海香洲二模)对于抛物线y = 3(x - 2)² - 1，下列说法正确的是(M9201002) ( )
A.y随x的增大而减小
B.当x = 2时，y有最大值，为-1
C.若点A(3,y₁),B(1,y₂)都在抛物线y = 3(x - 2)² - 1上，则y₁＞y₂
D.抛物线经过第一、二、四象限

答案： D   $\because y = 3(x - 2)^2 - 1$，$3＞0$，$\therefore$ 当 $x＜2$ 时，$y$ 随 $x$ 的增大而减小，当 $x＞2$ 时，$y$ 随 $x$ 的增大而增大，故选项 A 说法错误. $\because$ 抛物线 $y = 3(x - 2)^2 - 1$ 开口向上，$\therefore$ 当 $x = 2$ 时，$y$ 取最小值，为 -1，故选项 B 说法错误. $\because$ 抛物线的对称轴是直线 $x = 2$，$|3 - 2| = |1 - 2|$，$\therefore$ 点 $A$，$B$ 关于抛物线的对称轴对称，$\therefore y_1 = y_2$，故选项 C 说法错误. $\because$ 当 $x＜2$ 时，$y$ 随 $x$ 的增大而减小，且当 $x = 0$ 时，$y = 11$，$\therefore$ 当 $x＜0$ 时，$y＞11$，$\therefore$ 抛物线不经过第三象限，抛物线经过第一、二、四象限，故选项 D 说法正确，符合题意. 故选 D.

7.(2024广东广州中考)如图，在⊙O中，弦AB的长为4$\sqrt{3}$，点C在⊙O上，OC⊥AB，∠ABC = 30°.⊙O所在的平面内有一点P，若OP = 5，则点P与⊙O的位置关系是(M9202001) ( )

A.点P在⊙O上
B.点P在⊙O内
C.点P在⊙O外
D.无法确定

答案： C  设 $AB$ 与 $OC$ 交于点 $D$，$\because$ 弦 $AB$ 的长为 $4\sqrt{3}$，$OC\perp AB$，$\therefore AD = BD = \frac{1}{2}AB = 2\sqrt{3}$，$\because \angle ABC = 30^{\circ}$，$\therefore \angle AOD = 2\angle ABC = 60^{\circ}$，$\therefore \angle OAB = 90^{\circ} - 60^{\circ} = 30^{\circ}$，$\therefore OA = 2OD$. 设 $OD = x$，则 $OA = 2x$，在 $Rt\triangle AOD$ 中，$OD^2 + AD^2 = OA^2$，$\therefore x^2 + (2\sqrt{3})^2 = (2x)^2$，解得 $x = 2$ 或 $x = -2$（舍去），$\therefore OA = 2x = 4$. $\because OP = 5$，$\therefore OP＞OA$，$\therefore$ 点 $P$ 在 $\odot O$ 外. 故选 C.