第59页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
1.(2024 陕西西安模拟)某物理兴趣小组对一款饮水机的工作电路展开研究,如图①,将变阻器R的滑片从一端滑到另一端,绘制出变阻器R的电功率P随电流I变化的关系图象,如图②所示,且该图象是经过原点的一条抛物线的一部分,则变阻器R的电功率P最大为 ( )
A.160 W B.180 W C.200 W D.220 W
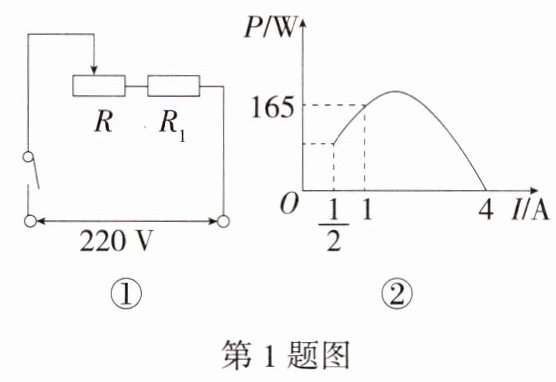
A.160 W B.180 W C.200 W D.220 W

答案:
D 因为图象是经过原点的一条抛物线的一部分,所以设抛物线的表达式为$P = aI^{2}+bI$,把$(1,165)$,$(4,0)$代入,得$\begin{cases}a + b=165\\16a + 4b = 0\end{cases}$,解得$\begin{cases}a=-55\\b = 220\end{cases}$。\n所以抛物线的表达式为$P=-55I^{2}+220I=-55(I - 2)^{2}+220$。因为$-55\lt0$,所以当$I = 2$时,$P$取最大值,为$220$,所以变阻器$R$的电功率$P$最大为$220W$。故选 D。
2.(2023 北京交大附中诊断)如图,在某足球比赛中,甲带球奔向对方球门PQ,当他带球冲到点A时,同伴乙已经助攻冲到点B,此时有两种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门.仅从射门角度考虑,应选择第________种射门方式比较好.(M9202003)


答案:
二 **解析**:如图,设$AP$与圆的交点为$C$,连接$CQ$,则$\angle PCQ\gt\angle A$,$\angle PCQ=\angle B$,所以$\angle B\gt\angle A$,因此选择第二种射门方式比较好。
二 **解析**:如图,设$AP$与圆的交点为$C$,连接$CQ$,则$\angle PCQ\gt\angle A$,$\angle PCQ=\angle B$,所以$\angle B\gt\angle A$,因此选择第二种射门方式比较好。

3.(2024 陕西咸阳永寿一模)唐代李皋发明了“桨轮船”,这种船是原始形态的轮船.如图,某桨轮船的轮子被水面截得的弦AB长6 m,轮子吃水的深度CD为1 m,则该桨轮船轮子的直径是 ( )
A.10 m B.8 m C.5 m D.4 m
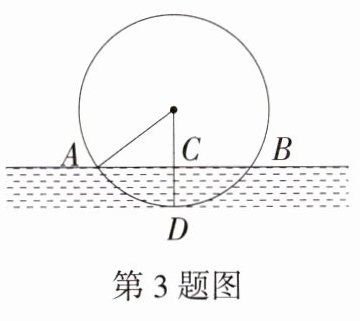
A.10 m B.8 m C.5 m D.4 m

答案:
A 设圆心为$O$,$OA = OD=r\ m$。因为$OD\perp AB$,所以$AC = CB = 3m$,因为$CD = 1m$,所以$OC=(r - 1)m$,在$Rt\triangle AOC$中,$OA^{2}=OC^{2}+AC^{2}$,即$r^{2}=(r - 1)^{2}+3^{2}$,解得$r = 5$,故该桨轮船轮子的直径是$10m$。故选 A。
4.(2024 湖北荆州一模)古希腊数学家曾给出一个估算地球周长(或子午圈长)的简单方法:如图,点A和点B分别表示埃及的西恩纳和亚历山大两地,B地在A地的北方,两地的经度大致相同,且实际距离($\overset{\frown}{AB}$的长)为800 km.当太阳光线在A地直射时,同一时刻在B地测量太阳光线偏离直射方向的角为$\alpha$,实际测得$\alpha$是7.2°,由此可估算地球周长,则地球周长用科学记数法表示为 ( )
A.4×10⁴ km B.2×10⁴ km
C.4×10³ km D.2×10⁵ km

A.4×10⁴ km B.2×10⁴ km
C.4×10³ km D.2×10⁵ km

答案:
A 如图,由题意得$OA// BC$,所以$\angle AOB=\alpha = 7.2^{\circ}$。设地球的半径为$r\ km$,因为$\overset{\frown}{AB}$的长为$800km$,所以$\frac{7.2\pi r}{180}=800$,则$\pi r=\frac{800\times180}{7.2}$。\n所以$2\pi r=\frac{2\times800\times180}{7.2}=40000 = 4\times10^{4}(km)$,所以估算地球周长为$4\times10^{4}km$,故选 A。
A 如图,由题意得$OA// BC$,所以$\angle AOB=\alpha = 7.2^{\circ}$。设地球的半径为$r\ km$,因为$\overset{\frown}{AB}$的长为$800km$,所以$\frac{7.2\pi r}{180}=800$,则$\pi r=\frac{800\times180}{7.2}$。\n所以$2\pi r=\frac{2\times800\times180}{7.2}=40000 = 4\times10^{4}(km)$,所以估算地球周长为$4\times10^{4}km$,故选 A。

5.(2024 广东深圳龙岗33校联考三模)苯(分子式为C₆H₆)的环状结构是由德国化学家凯库勒提出的.随着研究的不断深入,发现苯分子中的6个碳原子组成了一个完美的正六边形(如图①),图②是其平面示意图,点O为正六边形ABCDEF的中心,则∠CBF - ∠COD的度数为 ( )
A.30° B.45° C.60° D.90°
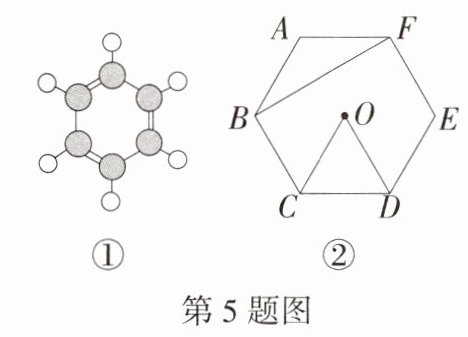
A.30° B.45° C.60° D.90°

答案:
**A**\n因为六边形$ABCDEF$是正六边形,所以$\angle A=\angle ABC=\frac{(6 - 2)\times180^{\circ}}{6}=120^{\circ}$,因为$AB = AF$,所以$\angle ABF=\frac{180^{\circ}-120^{\circ}}{2}=30^{\circ}$,所以$\angle CBF=\angle ABC-\angle ABF=120^{\circ}-30^{\circ}=90^{\circ}$。\n因为$\angle COD=\frac{360^{\circ}}{6}=60^{\circ}$,所以$\angle CBF-\angle COD=90^{\circ}-60^{\circ}=30^{\circ}$。故选 A。
6.(2024 湖北孝感云梦一中一模)公元前四世纪,希腊哲学家、科学史家欧德莫斯曾研究过对数学发展有重要影响的如下问题:如图,AB为⊙O的直径,过圆心O作OC⊥AB交⊙O于点C,以C为圆心,CA的长为半径作$\overset{\frown}{AB}$,若$S_{阴影}=4\ cm^{2}$,则$S_{\triangle ABC}=$________$cm^{2}$.(M9202006)
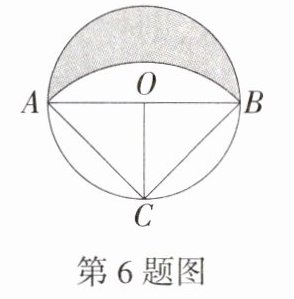

答案:
4 **解析**:因为$AB$为$\odot O$的直径,所以$\angle ACB = 90^{\circ}$,设$\odot O$的半径为$r\ cm$,则$AC=\sqrt{OA^{2}+OC^{2}}=\sqrt{2}r\ cm$。\n所以$S_{阴影}=\frac{1}{2}\pi r^{2}-(S_{扇形ACB}-S_{\triangle ABC})=\frac{1}{2}\pi r^{2}-\left[\frac{90\pi\times(\sqrt{2}r)^{2}}{360}-\frac{1}{2}\times2r\times r\right]=4(cm^{2})$,所以$r^{2}=4$。\n所以$S_{\triangle ABC}=\frac{1}{2}\times2r\times r=r^{2}=4cm^{2}$。
查看更多完整答案,请扫码查看


