第38页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
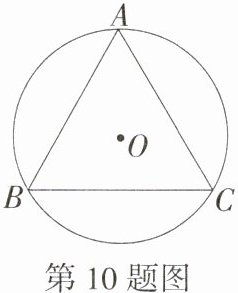
10.(2022湖南邵阳中考,9,★★☆)如图,⊙O是等边△ABC的外接圆,若AB = 3,则⊙O的半径是(M9202004)( )
A.$\frac{3}{2}$
B.$\frac{\sqrt{3}}{2}$
C.$\sqrt{3}$
D.$\frac{5}{2}$

A.$\frac{3}{2}$
B.$\frac{\sqrt{3}}{2}$
C.$\sqrt{3}$
D.$\frac{5}{2}$
答案:
C:连接 OB,过 O 点作 OE⊥BC 于点 E,易得 BO 平分∠ABC,
∴∠OBE = 30°.
∵OE⊥BC,
∴BE = $\frac{1}{2}BC=\frac{1}{2}AB=\frac{3}{2}$. 在 Rt△OBE 中,cos∠OBE = $\frac{BE}{OB}$,
∴$\frac{\frac{3}{2}}{OB}=\frac{\sqrt{3}}{2}$,解得 OB = $\sqrt{3}$,即⊙O 的半径为$\sqrt{3}$,故选 C.
∴∠OBE = 30°.
∵OE⊥BC,
∴BE = $\frac{1}{2}BC=\frac{1}{2}AB=\frac{3}{2}$. 在 Rt△OBE 中,cos∠OBE = $\frac{BE}{OB}$,
∴$\frac{\frac{3}{2}}{OB}=\frac{\sqrt{3}}{2}$,解得 OB = $\sqrt{3}$,即⊙O 的半径为$\sqrt{3}$,故选 C.
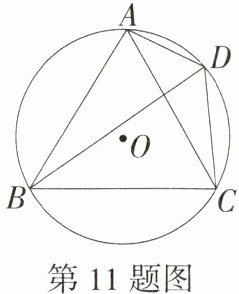
11.(2024湖南益阳沅江两校一模,9,★★☆)如图,⊙O是等边△ABC的外接圆,点D是弧AC上一动点(不与A,C重合),有下列结论:①∠ADB = ∠BDC;②DA = DC;③当DB最长时,DB = 2DC;④DA + DC = DB.其中一定正确的结论有(M9202004)( )
A.1个
B.2个
C.3个
D.4个

A.1个
B.2个
C.3个
D.4个
答案:
C:
∵△ABC 是等边三角形,
∴∠BAC = ∠ACB = 60°.
∵$\overset{\frown}{AB}=\overset{\frown}{AB}$,$\overset{\frown}{BC}=\overset{\frown}{BC}$,
∴∠ADB = ∠ACB = 60°,∠BDC = ∠BAC = 60°,
∴∠ADB = ∠BDC,故①正确.
∵点 D 是弧 AC 上一动点,
∴$\overset{\frown}{AD}$与$\overset{\frown}{CD}$不一定相等,
∴DA 与 DC 不一定相等,故②错误. 当 DB 最长时,DB 为⊙O 的直径,此时∠BCD = 90°,
∵∠BDC = 60°,
∴∠DBC = 30°,
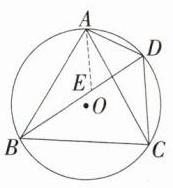
∴DB = 2DC,故③正确. 在 DB 上取一点 E,使 DE = AD,如图,
∵∠ADB = 60°,
∴△ADE 是等边三角形,
∴AD = AE,∠DAE = 60°,
∵∠BAC = 60°,
∴∠BAE = ∠CAD. 又
∵AB = AC,
∴△ABE≌△ACD(SAS),
∴BE = CD,
∴BD = BE + DE = CD + AD,故④正确. 综上,一定正确的结论有①③④,共 3 个,故选 C.
C:
∵△ABC 是等边三角形,
∴∠BAC = ∠ACB = 60°.
∵$\overset{\frown}{AB}=\overset{\frown}{AB}$,$\overset{\frown}{BC}=\overset{\frown}{BC}$,
∴∠ADB = ∠ACB = 60°,∠BDC = ∠BAC = 60°,
∴∠ADB = ∠BDC,故①正确.
∵点 D 是弧 AC 上一动点,
∴$\overset{\frown}{AD}$与$\overset{\frown}{CD}$不一定相等,
∴DA 与 DC 不一定相等,故②错误. 当 DB 最长时,DB 为⊙O 的直径,此时∠BCD = 90°,
∵∠BDC = 60°,
∴∠DBC = 30°,
∴DB = 2DC,故③正确. 在 DB 上取一点 E,使 DE = AD,如图,
∵∠ADB = 60°,
∴△ADE 是等边三角形,
∴AD = AE,∠DAE = 60°,
∵∠BAC = 60°,
∴∠BAE = ∠CAD. 又
∵AB = AC,
∴△ABE≌△ACD(SAS),
∴BE = CD,
∴BD = BE + DE = CD + AD,故④正确. 综上,一定正确的结论有①③④,共 3 个,故选 C.

12.[易错题](2024黑龙江哈尔滨南岗一模,19,★★☆)等腰△ABC内接于⊙O,若⊙O的半径为10,等腰△ABC的底边长为12,则这个等腰三角形的腰长AB = ________.(M9202004)
答案:
2$\sqrt{10}$或 6$\sqrt{10}$
解析:假设等腰△ABC 中,底边为 BC(底边为 AC、AB 时情况类似). 连接 OB,过 O 点作 OD⊥BC 于点 D,则 BD = CD = $\frac{1}{2}BC = 6$,OD 垂直平分 BC,
∵AB = AC,
∴点 A 在直线 OD 上,即点 A、O、D 共线,在 Rt△BOD 中,OB = 10,BD = 6,
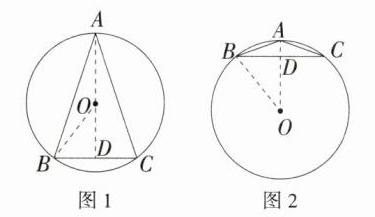
∴OD = $\sqrt{OB^{2}-BD^{2}} = 8$. 当△ABC 为锐角三角形时,如图 1,AD = OD + AO = 8 + 10 = 18,在 Rt△ABD 中,AB = $\sqrt{BD^{2}+AD^{2}} = 6\sqrt{10}$. 当△ABC 为钝角三角形时,如图 2,AD = AO - OD = 10 - 8 = 2,在 Rt△ABD 中,AB = $\sqrt{BD^{2}+AD^{2}} = 2\sqrt{10}$. 综上可知,这个等腰三角形的腰长为 2$\sqrt{10}$或 6$\sqrt{10}$.
2$\sqrt{10}$或 6$\sqrt{10}$
解析:假设等腰△ABC 中,底边为 BC(底边为 AC、AB 时情况类似). 连接 OB,过 O 点作 OD⊥BC 于点 D,则 BD = CD = $\frac{1}{2}BC = 6$,OD 垂直平分 BC,
∵AB = AC,
∴点 A 在直线 OD 上,即点 A、O、D 共线,在 Rt△BOD 中,OB = 10,BD = 6,
∴OD = $\sqrt{OB^{2}-BD^{2}} = 8$. 当△ABC 为锐角三角形时,如图 1,AD = OD + AO = 8 + 10 = 18,在 Rt△ABD 中,AB = $\sqrt{BD^{2}+AD^{2}} = 6\sqrt{10}$. 当△ABC 为钝角三角形时,如图 2,AD = AO - OD = 10 - 8 = 2,在 Rt△ABD 中,AB = $\sqrt{BD^{2}+AD^{2}} = 2\sqrt{10}$. 综上可知,这个等腰三角形的腰长为 2$\sqrt{10}$或 6$\sqrt{10}$.

13.(2022广西玉林中考,17,★★☆)如图,在5×7的网格中,小正方形的边长均为1,O,A,B,C,D,E均在格点上,点O是△ABC的外心,在不添加其他字母的情况下,除△ABC外把你认为外心也是O点的三角形都写出来:________.(M9202004)
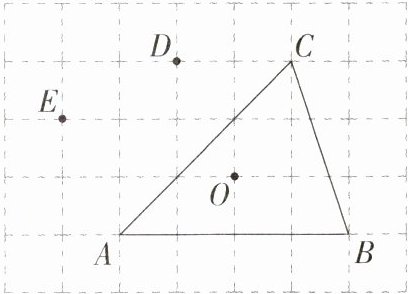

答案:
△ABD,△ACD,△BCD
解析:由题图可知,OA = $\sqrt{1^{2}+2^{2}}=\sqrt{5}$,OB = $\sqrt{1^{2}+2^{2}}=\sqrt{5}$,OC = $\sqrt{1^{2}+2^{2}}=\sqrt{5}$,OD = $\sqrt{1^{2}+2^{2}}=\sqrt{5}$,OE = $\sqrt{1^{2}+3^{2}}=\sqrt{10}$,
∴OA = OB = OC = OD≠OE,
∴△ABD,△ACD,△BCD 的外心都是 O 点.
解析:由题图可知,OA = $\sqrt{1^{2}+2^{2}}=\sqrt{5}$,OB = $\sqrt{1^{2}+2^{2}}=\sqrt{5}$,OC = $\sqrt{1^{2}+2^{2}}=\sqrt{5}$,OD = $\sqrt{1^{2}+2^{2}}=\sqrt{5}$,OE = $\sqrt{1^{2}+3^{2}}=\sqrt{10}$,
∴OA = OB = OC = OD≠OE,
∴△ABD,△ACD,△BCD 的外心都是 O 点.
14.(2024湖南常德澧县期末,22,★★☆)如图,⊙O是Rt△ABC的外接圆,∠ABC = 90°,BE平分∠ABC交⊙O于点E.(M9202004)
(1)若AB = BE,求证:∠BCA = ∠BAE;
(2)若AB = 12,BC = 5,求AE的长度.

(1)若AB = BE,求证:∠BCA = ∠BAE;
(2)若AB = 12,BC = 5,求AE的长度.

答案:
解析:
(1)证明:
∵AB = BE,
∴∠BEA = ∠BAE,
∵∠BCA = ∠BEA,
∴∠BCA = ∠BAE.
(2)在 Rt△ABC 中,AB = 12,BC = 5,∠ABC = 90°,
∴AC = $\sqrt{AB^{2}+BC^{2}} = 13$,AC 是⊙O 的直径,
∴∠AEC = 90°,
∵BE 平分∠ABC,
∴∠CBE = ∠ABE,
∴$\overset{\frown}{CE}=\overset{\frown}{AE}$,
∴CE = AE,
∴△AEC 是等腰直角三角形,
∴CE = AE = $\frac{\sqrt{2}}{2}AC=\frac{13\sqrt{2}}{2}$.
(1)证明:
∵AB = BE,
∴∠BEA = ∠BAE,
∵∠BCA = ∠BEA,
∴∠BCA = ∠BAE.
(2)在 Rt△ABC 中,AB = 12,BC = 5,∠ABC = 90°,
∴AC = $\sqrt{AB^{2}+BC^{2}} = 13$,AC 是⊙O 的直径,
∴∠AEC = 90°,
∵BE 平分∠ABC,
∴∠CBE = ∠ABE,
∴$\overset{\frown}{CE}=\overset{\frown}{AE}$,
∴CE = AE,
∴△AEC 是等腰直角三角形,
∴CE = AE = $\frac{\sqrt{2}}{2}AC=\frac{13\sqrt{2}}{2}$.
15.[推理能力](2024湖南长沙教科院模拟)正弦定理在高中数学中有很广泛的运用,下面先探索正弦定理,然后尝试应用正弦定理解决问题.(M9202004)
(1)在△ABC中,顶点A,B,C所对的边分别为a,b,c,记△ABC的外接圆半径为r,求证:$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2r$.(本题图未给出)
(2)如图,在等边三角形ABC中,D,E分别为边BC,AC上的点,且满足AE = CD,过B点作AD的垂线交AD于点F,设AD与BE交于点G,若GF = x,GE = y,求△ACD的外接圆半径(用含x,y的式子表示).

(1)在△ABC中,顶点A,B,C所对的边分别为a,b,c,记△ABC的外接圆半径为r,求证:$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2r$.(本题图未给出)
(2)如图,在等边三角形ABC中,D,E分别为边BC,AC上的点,且满足AE = CD,过B点作AD的垂线交AD于点F,设AD与BE交于点G,若GF = x,GE = y,求△ACD的外接圆半径(用含x,y的式子表示).

答案:
解析:
(1)证明:如图,作△ABC 的外接圆⊙O,作⊙O 的直径 AD,连接 BD,则 AD = 2r,∠ABD = 90°,
∵∠ABD = 90°,∠D = ∠C,AB = c,
∴$\frac{AB}{AD}=\sin D=\sin C$,
∴$\frac{c}{\sin C}=2r$. 同理,$\frac{a}{\sin A}=2r$,$\frac{b}{\sin B}=2r$,
∴$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2r$.
(2)
∵△ABC 是等边三角形,
∴AB = CA,∠BAE = ∠C = 60°. 在△ABE 和△CAD 中,$\begin{cases}AB = CA\\\angle BAE = \angle C\\AE = CD\end{cases}$,
∴△ABE≌△CAD(SAS),
∴BE = AD,∠ABE = ∠CAD,
∴∠BGD = ∠BAD + ∠ABE = ∠BAD + ∠CAD = ∠BAC = 60°.
∵BF⊥AD,
∴∠BFG = 90°,
∴∠FBG = 90° - ∠BGD = 30°,
∴BG = 2GF = 2x,
∴AD = BE = BG + GE = 2x + y,设△ACD 的外接圆的半径为 r,则$\frac{AD}{\sin C}=2r$,
∴$\frac{2x + y}{\frac{\sqrt{3}}{2}}=2r$,
∴r = $\frac{2\sqrt{3}}{3}x+\frac{\sqrt{3}}{3}y$,
∴△ACD 的外接圆半径为$\frac{2\sqrt{3}}{3}x+\frac{\sqrt{3}}{3}y$.

解析:
(1)证明:如图,作△ABC 的外接圆⊙O,作⊙O 的直径 AD,连接 BD,则 AD = 2r,∠ABD = 90°,
∵∠ABD = 90°,∠D = ∠C,AB = c,
∴$\frac{AB}{AD}=\sin D=\sin C$,
∴$\frac{c}{\sin C}=2r$. 同理,$\frac{a}{\sin A}=2r$,$\frac{b}{\sin B}=2r$,
∴$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2r$.
(2)
∵△ABC 是等边三角形,
∴AB = CA,∠BAE = ∠C = 60°. 在△ABE 和△CAD 中,$\begin{cases}AB = CA\\\angle BAE = \angle C\\AE = CD\end{cases}$,
∴△ABE≌△CAD(SAS),
∴BE = AD,∠ABE = ∠CAD,
∴∠BGD = ∠BAD + ∠ABE = ∠BAD + ∠CAD = ∠BAC = 60°.
∵BF⊥AD,
∴∠BFG = 90°,
∴∠FBG = 90° - ∠BGD = 30°,
∴BG = 2GF = 2x,
∴AD = BE = BG + GE = 2x + y,设△ACD 的外接圆的半径为 r,则$\frac{AD}{\sin C}=2r$,
∴$\frac{2x + y}{\frac{\sqrt{3}}{2}}=2r$,
∴r = $\frac{2\sqrt{3}}{3}x+\frac{\sqrt{3}}{3}y$,
∴△ACD 的外接圆半径为$\frac{2\sqrt{3}}{3}x+\frac{\sqrt{3}}{3}y$.

查看更多完整答案,请扫码查看


