第35页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
9.教材变式·P60T4如图,在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D.
(1)求证:AC = BD;
(2)若大圆的半径R = 10,小圆的半径r = 8,且圆心O到直线AB的距离为6,求AC的长.

(1)求证:AC = BD;
(2)若大圆的半径R = 10,小圆的半径r = 8,且圆心O到直线AB的距离为6,求AC的长.

答案:
解析 \n(1)证明:如图,过$O$点作$OE \perp AB$于点$E$,则$CE = DE$,$AE = BE$,$\therefore AE - CE = BE - DE$,即$AC = BD$.\n(2)由(1)可知$OE \perp AB$且$OE \perp CD$,连接$OC$,$OA$,如图,$\because OE = 6$,$\therefore CE=\sqrt{OC^{2}-OE^{2}}=\sqrt{8^{2}-6^{2}} = 2\sqrt{7}$,$AE=\sqrt{OA^{2}-OE^{2}}=\sqrt{10^{2}-6^{2}} = 8$,$\therefore AC = AE - CE = 8 - 2\sqrt{7}$.

解析 \n(1)证明:如图,过$O$点作$OE \perp AB$于点$E$,则$CE = DE$,$AE = BE$,$\therefore AE - CE = BE - DE$,即$AC = BD$.\n(2)由(1)可知$OE \perp AB$且$OE \perp CD$,连接$OC$,$OA$,如图,$\because OE = 6$,$\therefore CE=\sqrt{OC^{2}-OE^{2}}=\sqrt{8^{2}-6^{2}} = 2\sqrt{7}$,$AE=\sqrt{OA^{2}-OE^{2}}=\sqrt{10^{2}-6^{2}} = 8$,$\therefore AC = AE - CE = 8 - 2\sqrt{7}$.

10.新考向·尺规作图(2023山西忻州五台期中)如图,AB是⊙O的直径,点P是AB上一点,且点P是弦CD的中点.(M9202003)
(1)依题意画出弦CD;(尺规作图不写作法,保留作图痕迹)
(2)若AP = 4,CD = 16,求⊙O的半径.

(1)依题意画出弦CD;(尺规作图不写作法,保留作图痕迹)
(2)若AP = 4,CD = 16,求⊙O的半径.

答案:
解析 \n(1)弦$CD$如图所示.\n(2)如图,连接$OD$,$\because P$是弦$CD$的中点,点$P$在直径$AB$上,$\therefore AB \perp CD$,$PD=\frac{1}{2}CD = 8$. 设$\odot O$的半径为$r$,则$OD = r$,$OP = OA - AP = r - 4$,在$\odot Rt \triangle ODP$中,$OD^{2}=OP^{2}+PD^{2}$,$\therefore r^{2}=(r - 4)^{2}+8^{2}$,解得$r = 10$,$\therefore \odot O$的半径为$10$.
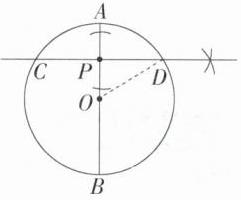
解析 \n(1)弦$CD$如图所示.\n(2)如图,连接$OD$,$\because P$是弦$CD$的中点,点$P$在直径$AB$上,$\therefore AB \perp CD$,$PD=\frac{1}{2}CD = 8$. 设$\odot O$的半径为$r$,则$OD = r$,$OP = OA - AP = r - 4$,在$\odot Rt \triangle ODP$中,$OD^{2}=OP^{2}+PD^{2}$,$\therefore r^{2}=(r - 4)^{2}+8^{2}$,解得$r = 10$,$\therefore \odot O$的半径为$10$.

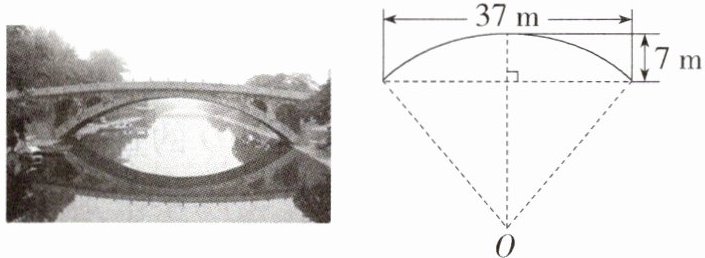
11.情境题·中华优秀传统文化(2023广西中考,10,★★☆)赵州桥是当今世界上建造最早、保存最完整的中国古代单孔敞肩石拱桥.如图,主桥拱呈圆弧形,跨度约为37 m,拱高约为7 m,则赵州桥主桥拱半径约为(M9202003) ( )
A.20 m
B.28 m
C.35 m
D.40 m

A.20 m
B.28 m
C.35 m
D.40 m
答案:
B 如图,由题意可知,$AB = 37\ \text{m}$,$CD = 7\ \text{m}$,设主桥拱半径为$r\ \text{m}$,$\therefore OD = OC - CD=(r - 7)\ \text{m}$,$\because OC$是半径,$OC \perp AB$,$\therefore AD = BD=\frac{1}{2}AB=\frac{37}{2}\ \text{m}$,在$\text{Rt} \triangle ADO$中,$AD^{2}+OD^{2}=OA^{2}$,$\therefore (\frac{37}{2})^{2}+(r - 7)^{2}=r^{2}$,解得$r=\frac{1565}{56}\approx28$,$\therefore$赵州桥主桥拱半径约为$28\ \text{m}$. 故选 B.
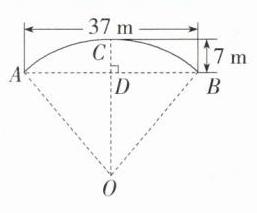
B 如图,由题意可知,$AB = 37\ \text{m}$,$CD = 7\ \text{m}$,设主桥拱半径为$r\ \text{m}$,$\therefore OD = OC - CD=(r - 7)\ \text{m}$,$\because OC$是半径,$OC \perp AB$,$\therefore AD = BD=\frac{1}{2}AB=\frac{37}{2}\ \text{m}$,在$\text{Rt} \triangle ADO$中,$AD^{2}+OD^{2}=OA^{2}$,$\therefore (\frac{37}{2})^{2}+(r - 7)^{2}=r^{2}$,解得$r=\frac{1565}{56}\approx28$,$\therefore$赵州桥主桥拱半径约为$28\ \text{m}$. 故选 B.

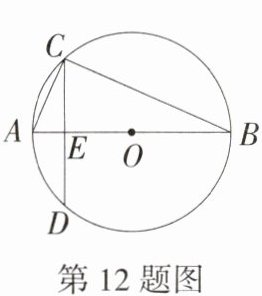
12.(2024湖南邵阳新宁模拟,10,★★☆)如图,已知AB是⊙O的直径,弦CD⊥AB,垂足为E,∠ACD = 22.5°,AB = 4,则CD的长为 ( )
A.$\sqrt{2}$
B.2
C.2$\sqrt{2}$
D.4$\sqrt{2}$

A.$\sqrt{2}$
B.2
C.2$\sqrt{2}$
D.4$\sqrt{2}$
答案:
C 连接$OD$,$\because AB$是$\odot O$的直径,弦$CD \perp AB$,$AB = 4$,$\therefore OD = 2$,$CE = DE=\frac{1}{2}CD$.$\because \angle ACD = 22.5^{\circ}$,$\therefore \angle AOD = 2\angle ACD = 45^{\circ}$,$\therefore \triangle DOE$为等腰直角三角形,$\therefore DE=\frac{\sqrt{2}}{2}OD=\sqrt{2}$,$\therefore CD = 2DE = 2\sqrt{2}$,故选 C.
13.方程思想(2024湖南岳阳汨罗弼时片区月考,9,★★☆)如图,在⊙O中,半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接EC,若AB = 8,CD = 2,则EC的长度为 ( )

A.2$\sqrt{15}$
B.8
C.2$\sqrt{10}$
D.2$\sqrt{13}$

A.2$\sqrt{15}$
B.8
C.2$\sqrt{10}$
D.2$\sqrt{13}$
答案:
D 连接$BE$,$\because OD \perp AB$,$\therefore AC = BC=\frac{1}{2}AB=\frac{1}{2}\times8 = 4$. 设$\odot O$的半径为$r$,则$OA = r$,$OC = r - 2$,$\because OC^{2}+AC^{2}=OA^{2}$,$\therefore (r - 2)^{2}+4^{2}=r^{2}$,解得$r = 5$,$\therefore OC = 5 - 2 = 3$,$\because O$是$AE$的中点,$C$是$AB$的中点,$\therefore OC$是$\triangle ABE$的中位线,$\therefore BE = 2OC = 6$.$\because AE$为$\odot O$的直径,$\therefore \angle ABE = 90^{\circ}$,在$\text{Rt} \triangle BCE$中,$CE=\sqrt{BC^{2}+BE^{2}} = 2\sqrt{13}$. 故选 D.
14.(2023湖南永州中考,18,★★☆)如图,⊙O是一个盛有水的容器的横截面,⊙O的半径为10 cm,水的最深处到水面AB的距离为4 cm,则水面AB的宽度为________cm.


答案:
$16$
解析 如图,过点$O$作$OD \perp AB$于点$C$,交$\odot O$于点$D$,连接$OA$,则$AC = BC=\frac{1}{2}AB$,由题意知,$OD = OA = 10\ \text{cm}$,$CD = 4\ \text{cm}$,$\therefore OC = 6\ \text{cm}$,在$\text{Rt} \triangle AOC$中,$AC=\sqrt{OA^{2}-OC^{2}}=\sqrt{10^{2}-6^{2}} = 8(\text{cm})$,$\therefore AB = 2AC = 16\ \text{cm}$.
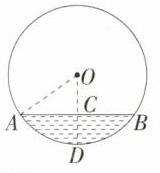
$16$
解析 如图,过点$O$作$OD \perp AB$于点$C$,交$\odot O$于点$D$,连接$OA$,则$AC = BC=\frac{1}{2}AB$,由题意知,$OD = OA = 10\ \text{cm}$,$CD = 4\ \text{cm}$,$\therefore OC = 6\ \text{cm}$,在$\text{Rt} \triangle AOC$中,$AC=\sqrt{OA^{2}-OC^{2}}=\sqrt{10^{2}-6^{2}} = 8(\text{cm})$,$\therefore AB = 2AC = 16\ \text{cm}$.

15.(2022湖南长沙中考,13,★★☆)如图,A、B、C是⊙O上的点,OC⊥AB,垂足为D,且D为OC的中点,若OA = 7,则BC的长为________.
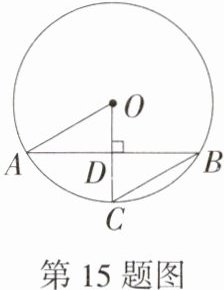

答案:
$7$
解析 $\because D$为$OC$的中点,$\therefore OD = CD$.$\because OC \perp AB$,$\therefore \angle ODA=\angle CDB = 90^{\circ}$,$AD = BD$. 在$\triangle AOD$和$\triangle BCD$中,$\begin{cases}OD = CD,\\\angle ADO=\angle BDC,\\AD = BD,\end{cases}$ $\therefore \triangle AOD\cong\triangle BCD(\text{SAS})$,$\therefore BC = OA = 7$.
解析 $\because D$为$OC$的中点,$\therefore OD = CD$.$\because OC \perp AB$,$\therefore \angle ODA=\angle CDB = 90^{\circ}$,$AD = BD$. 在$\triangle AOD$和$\triangle BCD$中,$\begin{cases}OD = CD,\\\angle ADO=\angle BDC,\\AD = BD,\end{cases}$ $\therefore \triangle AOD\cong\triangle BCD(\text{SAS})$,$\therefore BC = OA = 7$.
查看更多完整答案,请扫码查看


