第101页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
23.(答案含评分细则)(情境题·科学研究)(2024湖南邵阳武冈模拟)(9分)中国科学技术大学构建的量子计算原型机“九章”,求解数学算法高斯玻色取样只需200秒,这一突破使我国成为全球第二个实现“量子优越性”的国家.为了解初中生对量子计算的知晓情况,某数学兴趣小组在本校学生中开展了专题调查活动,随机抽取了部分学生进行问卷调查,根据学生的答题情况,将结果分为$A$,$B$,$C$,$D$四类,分别表示“非常了解”“比较了解”“基本了解”“不太了解”,并根据调查结果绘制了如下两幅尚不完整的统计图.
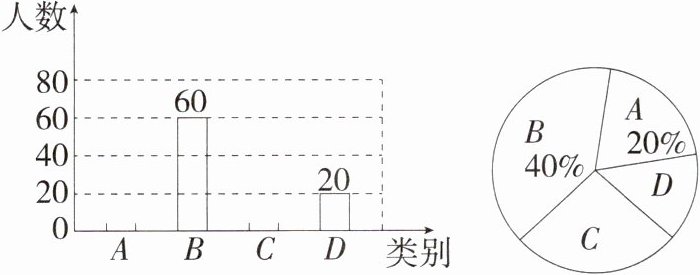
请根据以上信息,解答下列问题.
(1)本次一共调查了________名学生,补全条形统计图.
(2)若该校共有初中生3 000名,请你估计该校初中生对量子计算“基本了解”的人数.
(3)某班有四位同学(3男1女)非常了解量子计算,学校准备从中选2位同学参加知识问答竞赛,请利用画树状图或列表的方法,求恰好选中一男一女的概率.

请根据以上信息,解答下列问题.
(1)本次一共调查了________名学生,补全条形统计图.
(2)若该校共有初中生3 000名,请你估计该校初中生对量子计算“基本了解”的人数.
(3)某班有四位同学(3男1女)非常了解量子计算,学校准备从中选2位同学参加知识问答竞赛,请利用画树状图或列表的方法,求恰好选中一男一女的概率.
答案:
解析:(1)$60\div40\% = 150$(名),
即本次一共调查了 150 名学生, …… 1 分
$A$类人数为$150\times20\% = 30$,$C$类人数为$150 - 30 - 60 - 20 = 40$。补全条形统计图如图所示。

(2)$3000\times\frac{40}{150}=800$(名)。
答:估计该校初中生对量子计算“基本了解”的人数为 800。 …… 6 分
(3)画树状图如下:

共有 12 种等可能的结果,其中恰好选中一男一女的结果有 6 种,故恰好选中一男一女的概率为$\frac{6}{12}=\frac{1}{2}$。
…… 9 分
解析:(1)$60\div40\% = 150$(名),
即本次一共调查了 150 名学生, …… 1 分
$A$类人数为$150\times20\% = 30$,$C$类人数为$150 - 30 - 60 - 20 = 40$。补全条形统计图如图所示。

(2)$3000\times\frac{40}{150}=800$(名)。
答:估计该校初中生对量子计算“基本了解”的人数为 800。 …… 6 分
(3)画树状图如下:

共有 12 种等可能的结果,其中恰好选中一男一女的结果有 6 种,故恰好选中一男一女的概率为$\frac{6}{12}=\frac{1}{2}$。
…… 9 分
24.(答案含评分细则)(新考向·项目式学习试题)(2024湖南中考)(9分)某数学研究性学习小组在老师的指导下,利用课余时间进行测量活动.
|活动主题|测算某水池中雕塑底座的底面积|
|--|--|
|测量工具|皮尺、测角仪、计算器等|
|模型抽象|某休闲广场的水池中有一雕塑,其底座的底面为矩形$ABCD$,其示意图如下: |
|
|活动过程测绘过程与数据信息|①在水池外取一点$E$,使得点$C$,$B$,$E$在同一条直线上;
②过点$E$作$GH\perp CE$,并沿$EH$方向前进到点$F$,用皮尺测得$EF$的长为4米;
③在点$F$处用测角仪测得$\angle CFG = 60.3^{\circ}$,$\angle BFG = 45^{\circ}$,$\angle AFG = 21.8^{\circ}$;
④用计算器计算,得$\sin60.3^{\circ}\approx0.87$,$\cos60.3^{\circ}\approx0.50$,$\tan60.3^{\circ}\approx1.75$,$\sin21.8^{\circ}\approx0.37$,$\cos21.8^{\circ}\approx0.93$,$\tan21.8^{\circ}\approx0.40$|
请根据表格中提供的信息,解决下列问题(结果保留整数).
(1)求线段$CE$和$BC$的长度.
(2)求底座的底面$ABCD$的面积.
|活动主题|测算某水池中雕塑底座的底面积|
|--|--|
|测量工具|皮尺、测角仪、计算器等|
|模型抽象|某休闲广场的水池中有一雕塑,其底座的底面为矩形$ABCD$,其示意图如下:
 |
||活动过程测绘过程与数据信息|①在水池外取一点$E$,使得点$C$,$B$,$E$在同一条直线上;
②过点$E$作$GH\perp CE$,并沿$EH$方向前进到点$F$,用皮尺测得$EF$的长为4米;
③在点$F$处用测角仪测得$\angle CFG = 60.3^{\circ}$,$\angle BFG = 45^{\circ}$,$\angle AFG = 21.8^{\circ}$;
④用计算器计算,得$\sin60.3^{\circ}\approx0.87$,$\cos60.3^{\circ}\approx0.50$,$\tan60.3^{\circ}\approx1.75$,$\sin21.8^{\circ}\approx0.37$,$\cos21.8^{\circ}\approx0.93$,$\tan21.8^{\circ}\approx0.40$|
请根据表格中提供的信息,解决下列问题(结果保留整数).
(1)求线段$CE$和$BC$的长度.
(2)求底座的底面$ABCD$的面积.
答案:
解析:(1)$\because GH\perp CE$,$EF = 4$米,$\angle CFG = 60.3^{\circ}$,
$\therefore \tan\angle CFE=\tan60.3^{\circ}=\frac{CE}{EF}\approx1.75$,
$\therefore CE\approx7$米。 …… 3 分
$\because \angle BFG = 45^{\circ}$,$\therefore BE = EF = 4$米,
$\therefore BC = CE - BE = 7 - 4 = 3$(米)。 …… 5 分
(2)过点$A$作$AM\perp GH$于点$M$,如图所示。
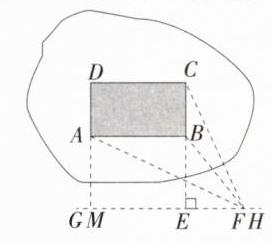
$\because \angle AFG = 21.8^{\circ}$,$\therefore \tan\angle AFG=\tan21.8^{\circ}=\frac{AM}{MF}\approx0.40$。
易知$AM = BE = 4$米,$\therefore MF\approx10$米,
$\therefore AB = ME = 10 - 4 = 6$(米), …… 8 分
$\therefore$底座的底面$ABCD$的面积为$3\times6 = 18$(平方米)。
…… 9 分
解析:(1)$\because GH\perp CE$,$EF = 4$米,$\angle CFG = 60.3^{\circ}$,
$\therefore \tan\angle CFE=\tan60.3^{\circ}=\frac{CE}{EF}\approx1.75$,
$\therefore CE\approx7$米。 …… 3 分
$\because \angle BFG = 45^{\circ}$,$\therefore BE = EF = 4$米,
$\therefore BC = CE - BE = 7 - 4 = 3$(米)。 …… 5 分
(2)过点$A$作$AM\perp GH$于点$M$,如图所示。

$\because \angle AFG = 21.8^{\circ}$,$\therefore \tan\angle AFG=\tan21.8^{\circ}=\frac{AM}{MF}\approx0.40$。
易知$AM = BE = 4$米,$\therefore MF\approx10$米,
$\therefore AB = ME = 10 - 4 = 6$(米), …… 8 分
$\therefore$底座的底面$ABCD$的面积为$3\times6 = 18$(平方米)。
…… 9 分
查看更多完整答案,请扫码查看


