《2025年5年中考3年模拟九年级数学下册湘教版》

1.（2023 湖北武汉蔡甸期末）某种商品每天的销售利润$y$元与单价$x$元（$x\geq2$）之间的函数关系式为$y = -0.1(x - 3)^2 + 50$，则这种商品每天的销售利润最大为（ ）
A.1元
B.3元
C.50元
D.75元

答案： C   $\because -0.1＜0$，$\therefore$ 当 $x = 3$ 时，$y$ 取得最大值，为 $50$，$\therefore$ 这种商品每天的销售利润最大为 $50$ 元. 故选 C.

2.（2024 湖南长沙岳麓长郡双语中学月考）某种商品每件的进价为30元，在某时间段内若以每件$x$元出售，可卖出$(100 - x)$件.若想获得最大利润，则每件的价格应为（ ）
A.35元
B.45元
C.55元
D.65元

答案：  D  设获得的利润为 $w$ 元，则 $w=(x - 30)(100 - x)=-(x - 65)^{2}+1225$，$\because -1＜0$，$30＜x＜100$，$\therefore$ 当 $x = 65$ 时，$w$ 有最大值，为 $1225$，$\therefore$ 每件的价格为 $65$ 元时，利润最大. 故选 D.

3. 新独家原创 湖南一家文化纪念品商店销售各种各样的纪念品，商店老板每周用5 000元购进一款特色纪念品，在销售过程中发现，每周的销售额$y$（元）与售价$x$（元/个）满足关系式$y = -x^2 + 100x + 9 500$，则当$x =$_______时，每周的利润最大，最大利润是_______元.

答案：  $50$；$7000$
**解析** 设每周获得的利润为 $w$ 元，则 $w = y - 5000=-x^{2}+100x + 9500 - 5000=-x^{2}+100x + 4500=-(x - 50)^{2}+7000$，$\because -1＜0$，$\therefore$ 当 $x = 50$ 时，$w$ 有最大值，为 $7000$，即当 $x = 50$ 时，每周的利润最大，最大利润是 $7000$ 元.

4.（2024 河南洛阳孟津期末）某花圃用花盆培育花苗，经试验发现，每盆的盈利与每盆种植的株数有一定的关系.每盆种植4株时，平均每株盈利4元，以同样的栽培条件，若每盆增加1株，平均单株盈利就减少0.5元.要使每盆盈利达到最大，则每盆应种植_______株.

答案：   $6$
**解析** 设每盆的盈利为 $y$ 元，每盆种植的株数为 $x$，则 $y=x[4-(x - 4)\times0.5]=6x - 0.5x^{2}=-0.5(x - 6)^{2}+18$，$\because -0.5＜0$，$\therefore$ 当 $x = 6$ 时，$y$ 有最大值，为 $18$，故要使每盆盈利达到最大，则每盆应种植 $6$ 株.

5. 情境题·社会主义先进文化 （2023 湖南长沙雅礼实验中学月考）为筹集救助基金，帮助孤独症儿童，校团委决定发起一场爱心义卖活动，义卖一种爱心纪念品.若纪念品以每件20元的价格销售，则每天能卖出360件；若以每件30元的价格销售，则每天仅能卖出60件.若每天的销售件数$y$是销售价格$x$（单位：元/件）的一次函数.
(1)求$y$关于$x$的函数解析式.
(2)若爱心纪念品每件的进价为10元，当销售价格定为多少元/件时，每天筹集的资金最多？并求出筹集资金的最大值.（注意：筹集的资金指的是当天的总利润）

答案： **解析**
(1) 设 $y = kx + b(k\neq0)$，把 $x = 20$，$y = 360$ 和 $x = 30$，$y = 60$ 分别代入，得 $\begin{cases}20k + b = 360\\30k + b = 60\end{cases}$，解得 $\begin{cases}k=-30\\b = 960\end{cases}$，$\therefore y=-30x + 960$.
(2) 设每天筹集的资金为 $W$ 元，则 $W=(-30x + 960)(x - 10)=-30(x - 32)(x - 10)=-30(x^{2}-42x + 320)=-30(x - 21)^{2}+3630$，$\because -30＜0$，$\therefore$ 当 $x = 21$ 时，$W$ 有最大值，最大值为 $3630$.
答：当销售价格定为 $21$ 元/件时，每天筹集的资金最多，为 $3630$ 元.

6.（2024 湖南常德一模，10，★☆☆）刀削面堪称天下一绝，传统的操作方法是一手托面，一手拿刀，直接将面削到开水锅里.如图，面刚被削离时与开水锅的高度差$h = 0.45$ m，与锅的水平距离$L = 0.3$ m，锅的半径$r = 0.5$ m.若将削出的面的运动轨迹视为抛物线的一部分，要使其落入锅中（锅的厚度忽略不计），则其水平初速度$v_0$不可能为（提示：$h=\frac{1}{2}gt^2$，$g = 10$ m/s²，水平移动距离$s = v_0t$）（ ）

A.2.5 m/s
B.3 m/s
C.3.5 m/s
D.5 m/s

答案：  D  $\because h=\frac{1}{2}gt^{2}$，$\therefore t=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2\times0.45}{10}} = 0.3(\text{s})$. 由题意易得 $L＜s＜L + 2r$，根据 $s = v_{0}t$，可得最小速度为 $\frac{L}{t}=\frac{0.3}{0.3}=1(\text{m/s})$，最大速度为 $\frac{L + 2r}{t}=\frac{0.3+2\times0.5}{0.3}=\frac{13}{3}(\text{m/s})$，选项 A，B，C 均在此范围内，不符合题意，选项 D 不在此范围内，符合题意，故选 D.

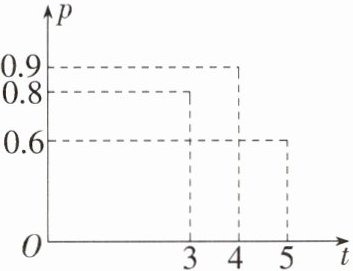
7. 湖南特色小吃·臭豆腐 （2020 湖南长沙中考，12，★☆☆）“闻起来臭，吃起来香”的臭豆腐是长沙特色小吃，臭豆腐虽小，但制作流程却比较复杂，其中在进行加工煎炸臭豆腐时，我们把“焦脆而不煳”的豆腐块数的百分比称为“可食用率”.在特定条件下，“可食用率”$p$与加工煎炸时间$t$（单位：分钟）近似满足的函数关系式为$p = at^2 + bt + c$（$a\neq0$，$a$，$b$，$c$是常数），下图记录了三次试验的数据.根据上述函数关系和试验数据，可以得到加工煎炸臭豆腐的最佳时间为（ ）

A.3.50分钟
B.4.05分钟
C.3.75分钟
D.4.25分钟

答案：  C  将题图中三个点 $(3,0.8)$，$(4,0.9)$，$(5,0.6)$ 的坐标代入 $p = at^{2}+bt + c$，得 $\begin{cases}9a + 3b + c = 0.8\\16a + 4b + c = 0.9\\25a + 5b + c = 0.6\end{cases}$，解得 $\begin{cases}a=-0.2\\b = 1.5\\c=-1.9\end{cases}$，$\therefore$ 函数关系式为 $p=-0.2t^{2}+1.5t - 1.9$，由题意可知，加工煎炸臭豆腐的最佳时间为抛物线顶点的横坐标 $t=-\frac{b}{2a}=-\frac{1.5}{2\times(-0.2)} = 3.75$，$\therefore$ 最佳时间为 $3.75$ 分钟. 故选 C.