《2025年5年中考3年模拟九年级数学下册湘教版》

1.(2023河北邯郸永年育英学校实验班月考)如图所示，PA，PB是⊙O的切线，且∠APB = 40°，下列说法不正确的是 ( )

A.PA = PB
B.∠APO = 20°
C.∠OBP = 70°
D.∠AOP = 70°

答案： C
∵ $PA$，$PB$ 是 $\odot O$ 的切线，$\angle APB = 40^{\circ}$，
∴ $PA = PB$，$\angle PAO=\angle PBO = 90^{\circ}$，$\angle APO=\angle BPO = 20^{\circ}$，
∴ $\angle AOP = 70^{\circ}$. 故选 C.

2.(2024湖南长沙雨花期末)如图，AB、AC、BD是⊙O的切线，切点分别是P、C、D.若AB = 5，AC = 3，则BD的长是 ( )

A.4
B.3
C.2
D.1

答案： C
∵ $AC$、$AP$ 为 $\odot O$ 的切线，
∴ $AP = AC = 3$，
∴ $BP=AB - AP = 5 - 3 = 2$.
∵ $BP$、$BD$ 为 $\odot O$ 的切线，
∴ $BD = BP = 2$. 故选 C.

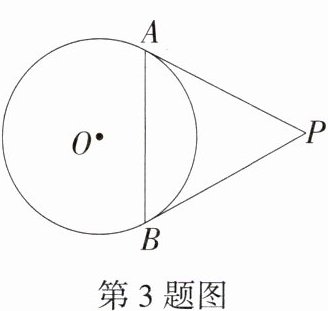
3.(2024湖南长沙望城模拟)如图，PA，PB与⊙O相切于点A，B，PA = 3，∠P = 60°，则AB = ______. (M9202005)

答案：   3
解析
∵ $PA$，$PB$ 与 $\odot O$ 相切于点 $A$，$B$，
∴ $PA = PB$. 又
∵ $\angle P = 60^{\circ}$，
∴ $\triangle APB$ 是等边三角形，
∴ $AB = PA = 3$.

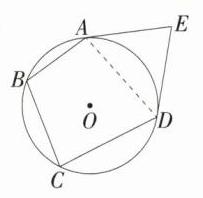
4.(2024四川泸州中考,9,★★☆)如图，EA，ED是⊙O的切线，切点为A，D，点B，C在⊙O上，若∠BAE + ∠BCD = 236°，则∠E = ( )

A.56°
B.60°
C.68°
D.70°

答案：
C
如图，连接 $AD$，
∵ 四边形 $ABCD$ 是 $\odot O$ 的内接四边形，
∴ $\angle BAD+\angle BCD = 180^{\circ}$，
∵ $\angle BAE+\angle BCD = 236^{\circ}$，
∴ $\angle EAD+\angle BAD+\angle BCD=\angle EAD + 180^{\circ}=236^{\circ}$，
∴ $\angle EAD = 56^{\circ}$，
∵ $EA$，$ED$ 是 $\odot O$ 的切线，
∴ $EA = ED$，
∴ $\angle EDA=\angle EAD = 56^{\circ}$，
∴ $\angle E = 180^{\circ}-\angle EDA-\angle EAD = 68^{\circ}$，故选 C.

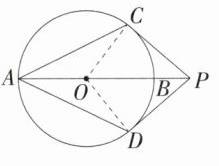
5.[等角替换法](2023湖南湘西州中考,10,★★☆)如图，AB为⊙O的直径，点P在AB的延长线上，PC，PD与⊙O相切，切点分别为C，D.若AB = 10，PC = 12，则sin∠CAD等于 ( )

A.$\frac{12}{5}$
B.$\frac{13}{12}$
C.$\frac{13}{5}$
D.$\frac{12}{13}$

答案：
D
如图，连接 $OC$，$OD$，
∵ $PC$，$PD$ 与 $\odot O$ 相切，
∴ $OC\perp CP$，$OD\perp DP$，易证 $\triangle COP\cong\triangle DOP$，
∴ $\angle COP=\angle DOP=\frac{1}{2}\angle COD$.
∵ $\angle CAD=\frac{1}{2}\angle COD$，
∴ $\angle CAD=\angle COP$.
∵ $AB = 10$，
∴ $OC=\frac{1}{2}AB = 5$，在 $Rt\triangle OCP$ 中，$OP=\sqrt{OC^{2}+PC^{2}}=\sqrt{5^{2}+12^{2}} = 13$，
∴ $\sin\angle CAD=\sin\angle COP=\frac{PC}{OP}=\frac{12}{13}$.
故选 D.

6.(2024广东惠州惠东二模,14,★★☆)如图，AB是⊙O的直径，C为⊙O外一点，CA，CD分别与⊙O相切于点A，D，连接BD，AD，若∠ACD = 50°，则∠DBA的度数是________. (M9202005)

答案：   $65^{\circ}$
解析
∵ $CA$，$CD$ 分别与 $\odot O$ 相切于点 $A$，$D$，
∴ $\angle CAO = 90^{\circ}$，$AC = CD$.
∵ $\angle ACD = 50^{\circ}$，
∴ $\angle CAD=\angle CDA = 65^{\circ}$，
∴ $\angle DAB = 90^{\circ}-\angle CAD = 25^{\circ}$.
∵ $AB$ 是 $\odot O$ 的直径，
∴ $\angle ADB = 90^{\circ}$，
∴ $\angle DBA = 90^{\circ}-\angle DAB=90^{\circ}-25^{\circ}=65^{\circ}$.

7.[情境题·数学文化](2022湖南株洲中考,18,★★☆)中国元代数学家朱世杰所著《四元玉鉴》记载有“锁套吞容”之“方田圆池结角池图”.“方田一段，一角圆池占之.”意思是说：一块正方形田地，在其一角有一个圆形的水池(其中圆与正方形一角的两边均相切)，如图所示.问题：此图中，正方形一条对角线AB与⊙O相交于点M、N(点N在点M的右上方)，若AB的长度为10丈，⊙O的半径为2丈，则BN的长度为______丈. (M9202005)

答案：   $(8 - 2\sqrt{2})$
解析 设正方形的边与 $\odot O$ 的一个切点为 $C$，连接 $OC$，则 $OC\perp AC$，由题易知 $\angle OAC = 45^{\circ}$，
∴ $OA=\sqrt{2}OC = 2\sqrt{2}$ 丈，
∴ $BN=AB - OA - ON = 10 - 2\sqrt{2}-2=(8 - 2\sqrt{2})$ 丈.

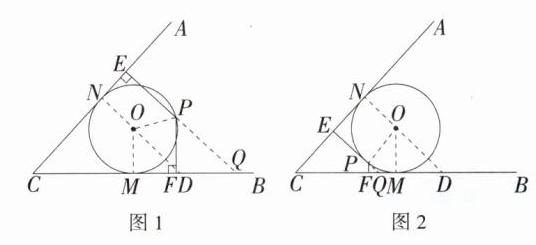
8.[推理能力](2024湖南长沙教科院模拟)如图，∠ACB = 45°，半径为2的⊙O与角的两边相切，点P是⊙O上任意一点，过点P向角的两边作垂线，垂足分别为E，F，设t = PE + $\sqrt{2}$PF，则t的取值范围是________.

答案：
  $2\sqrt{2}\leq t\leq4 + 2\sqrt{2}$
解析 设半径为 2 的 $\odot O$ 与角的两边 $CB$，$CA$ 相切于点 $M$，$N$，连接 $OM$，$ON$，延长 $NO$ 交 $CB$ 于点 $D$，
∴ $\angle CND=\angle OMD = 90^{\circ}$.
∵ $\angle ACB = 45^{\circ}$，
∴ $\angle CDN = 90^{\circ}-45^{\circ}=45^{\circ}=\angle ACB$，
∴ $CN = DN$，$\angle DOM = 90^{\circ}-45^{\circ}=45^{\circ}=\angle CDN$，
∴ $OM = MD$，
∵ $ON = OM = 2$，
∴ $OD = 2\sqrt{2}$，
∴ $CN = DN = 2 + 2\sqrt{2}$，
延长 $EP$ 交 $BC$ 于点 $Q$，如图 1，
∵ $EQ\perp AC$，$PF\perp BC$，
∴ $\angle CEQ=\angle PFQ = 90^{\circ}$.
∵ $\angle ACB = 45^{\circ}$，
∴ $\angle EQC = 90^{\circ}-45^{\circ}=45^{\circ}$，
∴ $\triangle ECQ$ 与 $\triangle PFQ$ 是等腰直角三角形，
∴ $CE = EQ$，$PQ=\sqrt{2}PF$，
∴ $t = PE+\sqrt{2}PF=PE + PQ = EQ$.
当 $EQ$ 与 $\odot O$ 相切且点 $P$ 在圆心的右上方时，$t$ 有最大值，
连接 $OP$，此时四边形 $ENOP$ 是正方形，
∴ $EN = OP = 2$，
∴ $t = PE+\sqrt{2}PF=PE + PQ = EQ = CE = CN+EN = 2 + 2\sqrt{2}+2=4 + 2\sqrt{2}$.
如图 2，当 $EQ$ 与 $\odot O$ 相切且点 $P$ 在圆心的左下方时，$t$ 有最小值，同理可得 $t = PE+\sqrt{2}PF=PE + PQ = EQ = CE = CN - EN = 2\sqrt{2}$.
故 $t$ 的取值范围是 $2\sqrt{2}\leq t\leq4 + 2\sqrt{2}$.