2025年初中毕业升学真题详解八年级数学上册北师大版陕西专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年初中毕业升学真题详解八年级数学上册北师大版陕西专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第1页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
1. 25的平方根是(
A.$\pm\sqrt{5}$
B.$\pm5$
C.$\sqrt{5}$
D.5
B
)。A.$\pm\sqrt{5}$
B.$\pm5$
C.$\sqrt{5}$
D.5
答案:
1. B [点拨]本题考查平方根的概念。
[解析]
∵(±5)² = 25,
∴25的平方根是±5。故选B。
[解析]
∵(±5)² = 25,
∴25的平方根是±5。故选B。
2. 下列函数中,表示$y$是$x$的正比例函数的是(
A.$y = -0.1x$
B.$y = 3x^2$
C.$y^2 = 4x$
D.$y = 5x + 1$
A
)。A.$y = -0.1x$
B.$y = 3x^2$
C.$y^2 = 4x$
D.$y = 5x + 1$
答案:
2. A [点拨]本题考查正比例函数的定义。
[解析]y = - 0.1x是正比例函数;y = 3x²不是正比例函数;y² = 4x不表示y是x的函数;y = 5x + 1是一次函数。故选A。
[解析]y = - 0.1x是正比例函数;y = 3x²不是正比例函数;y² = 4x不表示y是x的函数;y = 5x + 1是一次函数。故选A。
3. 下列化简错误的是(
A.$\frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}$
B.$\sqrt[3]{-27} = -3$
C.$(\sqrt{5})^0 = 1$
D.$\sqrt{(-4)^2} = -4$
D
)。A.$\frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}$
B.$\sqrt[3]{-27} = -3$
C.$(\sqrt{5})^0 = 1$
D.$\sqrt{(-4)^2} = -4$
答案:
3. D [点拨]本题考查二次根式、立方根、零指数幂的运算。
[解析]A. $\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$,故原选项计算正确,不符合题意;B. $\sqrt[3]{-27} = - 3$,故原选项计算正确,不符合题意;C. $(\sqrt{5})^{0} = 1$,故原选项计算正确,不符合题意;D. $\sqrt{(-4)^{2}} = 4$,故原选项计算错误,符合题意。故选D。
[解析]A. $\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$,故原选项计算正确,不符合题意;B. $\sqrt[3]{-27} = - 3$,故原选项计算正确,不符合题意;C. $(\sqrt{5})^{0} = 1$,故原选项计算正确,不符合题意;D. $\sqrt{(-4)^{2}} = 4$,故原选项计算错误,符合题意。故选D。
4. 平面直角坐标系内点$A(m,n)$在第二象限,则点$B(m,-n)$在(
A.第一象限
B.第二象限
C.第三象限
D.第四象限
C
)。A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案:
4. C [点拨]本题考查平面直角坐标系内点的坐标特征。
[解析]
∵点A(m,n)在第二象限,
∴m < 0,n > 0,
∴ - n < 0,
∴点B(m, - n)在第三象限。故选C。
[解析]
∵点A(m,n)在第二象限,
∴m < 0,n > 0,
∴ - n < 0,
∴点B(m, - n)在第三象限。故选C。
5. 估计$2 + \sqrt{5}$的大小应(
A.在$2\sim3$之间
B.在$3\sim4$之间
C.在$4\sim5$之间
D.在$5\sim6$之间
C
)。A.在$2\sim3$之间
B.在$3\sim4$之间
C.在$4\sim5$之间
D.在$5\sim6$之间
答案:
5. C [点拨]本题考查估算无理数的大小。
[解析]
∵4 < 5 < 9,
∴2 < $\sqrt{5}$ < 3,
∴4 < 2 + $\sqrt{5}$ < 5,
∴2 + $\sqrt{5}$的大小应在4~5之间。故选C。
[解析]
∵4 < 5 < 9,
∴2 < $\sqrt{5}$ < 3,
∴4 < 2 + $\sqrt{5}$ < 5,
∴2 + $\sqrt{5}$的大小应在4~5之间。故选C。
6. $\triangle ABC$的三边长分别为$a,b,c$,则下列条件不能判断$\triangle ABC$是直角三角形的是(
A.$\angle A = \angle B - \angle C$
B.$\angle A:\angle B:\angle C = 3:4:5$
C.$a^2 = (b + c)(b - c)$
D.$a:b:c = 5:12:13$
B
)。A.$\angle A = \angle B - \angle C$
B.$\angle A:\angle B:\angle C = 3:4:5$
C.$a^2 = (b + c)(b - c)$
D.$a:b:c = 5:12:13$
答案:
6. B [点拨]本题考查勾股定理逆定理及判定一个三角形是直角三角形。
[解析]A.
∵∠A = ∠B - ∠C,
∴∠B = ∠A + ∠C。
∵∠A + ∠B + ∠C = 180°,
∴2∠B = 180°,解得∠B = 90°,
∴△ABC是直角三角形,
∴此选项不符合题意;B.
∵∠A:∠B:∠C = 3:4:5,∠A + ∠B + ∠C = 180°,
∴∠C = 75°,
∴△ABC是锐角三角形,
∴此选项符合题意;C.
∵a² = (b + c)(b - c),
∴a² = b² - c²,
∴a² + c² = b²,
∴△ABC是直角三角形,
∴此选项不符合题意;D. 由a:b:c = 5:12:13,设a = 5x,b = 12x,c = 13x,
∴a² + b² = 169x² = c²,
∴△ABC是直角三角形,
∴此选项不符合题意。故选B。
[解析]A.
∵∠A = ∠B - ∠C,
∴∠B = ∠A + ∠C。
∵∠A + ∠B + ∠C = 180°,
∴2∠B = 180°,解得∠B = 90°,
∴△ABC是直角三角形,
∴此选项不符合题意;B.
∵∠A:∠B:∠C = 3:4:5,∠A + ∠B + ∠C = 180°,
∴∠C = 75°,
∴△ABC是锐角三角形,
∴此选项符合题意;C.
∵a² = (b + c)(b - c),
∴a² = b² - c²,
∴a² + c² = b²,
∴△ABC是直角三角形,
∴此选项不符合题意;D. 由a:b:c = 5:12:13,设a = 5x,b = 12x,c = 13x,
∴a² + b² = 169x² = c²,
∴△ABC是直角三角形,
∴此选项不符合题意。故选B。
7. 已知点$A(a + 1,3)$,点$B(3,a + 3)$,且直线$AB// y$轴,则$a$的值为(
A.2
B.1
C.$-2$
D.$-4$
A
)。A.2
B.1
C.$-2$
D.$-4$
答案:
7. A [点拨]本题考查平行于y轴的直线上点的坐标特征。
[解析]
∵点A(a + 1,3),点B(3,a + 3),且直线AB // y轴,
∴a + 1 = 3,解得a = 2。故选A。
[解析]
∵点A(a + 1,3),点B(3,a + 3),且直线AB // y轴,
∴a + 1 = 3,解得a = 2。故选A。
8. 右侧扫码·视频讲解 一次函数$y = kx + b$的图象如图所示,则一次函数$y = bx - k$的图象是(

A
)。
答案:
8. A [点拨]本题考查一次函数的图象与性质。
[解析]由一次函数y = kx + b的图象,得k < 0,b > 0,
∴ - k > 0,
为了方便广大师生和家长更全面地了解奎省初中阶段的教学资源,更好地架设起名校、学生、家长沟通的
九年级:语文、数学、英语、物理、化学、历史六科,各科期中、期末、中考考前冲刺模拟试卷,每份100元。
特别感谢:李老师、陈老师、王老师、张同学、梁同学以及刘妈妈、党妈妈等积极为我们提供试卷的朋友。
尊敬的读者朋友,您在使用本书的过程中,有任何问题都可以通过微信、QQ与我们联系,编辑老师会及时解答。本套书精心编辑加工,为防止疏漏,我们对第一个发现答案错误的读者予以奖励,并将正确答案及时更新。
∴一次函数y = bx - k的图象经过第一、二、三象限。故选A。
[解析]由一次函数y = kx + b的图象,得k < 0,b > 0,
∴ - k > 0,
为了方便广大师生和家长更全面地了解奎省初中阶段的教学资源,更好地架设起名校、学生、家长沟通的
九年级:语文、数学、英语、物理、化学、历史六科,各科期中、期末、中考考前冲刺模拟试卷,每份100元。
特别感谢:李老师、陈老师、王老师、张同学、梁同学以及刘妈妈、党妈妈等积极为我们提供试卷的朋友。
尊敬的读者朋友,您在使用本书的过程中,有任何问题都可以通过微信、QQ与我们联系,编辑老师会及时解答。本套书精心编辑加工,为防止疏漏,我们对第一个发现答案错误的读者予以奖励,并将正确答案及时更新。
∴一次函数y = bx - k的图象经过第一、二、三象限。故选A。
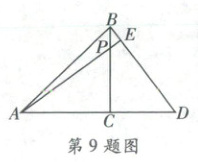
9. 右侧扫码·视频讲解 如图,在$ Rt\triangle ABC$中,$AC = BC = 4$,延长$AC$至点$D$,使$CD = 3$,连接$BD$,作$AE\perp BD$,垂足为$E$,$AE$交$BC$于点$P$,则$PE$的长度为(
A.1
B.$\frac{3}{5}$
C.2
D.$\frac{5}{2}$
B
)。
A.1
B.$\frac{3}{5}$
C.2
D.$\frac{5}{2}$
答案:
9. B [点拨]本题考查勾股定理及全等三角形的判定与性质。
[解析]
∵∠BCD = 90°,
∴BD² = BC² + CD² = 4² + 3² = 25,
∴BD = 5。
∵AD = AC + CD = 4 + 3 = 7,S△ABD = $\frac{1}{2}$AD·BC = $\frac{1}{2}$BD·AE,
∴7×4 = 5AE,解得AE = $\frac{28}{5}$。
∵AE⊥BD,AD⊥BC,
∴∠ACP = ∠BCD = ∠AED = 90°,
∴∠PAC + ∠APC = ∠PAC + ∠D,
∴∠APC = ∠D。又
∵AC = BC = 4,
∴△ACP≌△BCD(AAS),
∴AP = BD = 5,
∴PE = AE - AP = $\frac{28}{5}$ - 5 = $\frac{3}{5}$。故选B。
[解析]
∵∠BCD = 90°,
∴BD² = BC² + CD² = 4² + 3² = 25,
∴BD = 5。
∵AD = AC + CD = 4 + 3 = 7,S△ABD = $\frac{1}{2}$AD·BC = $\frac{1}{2}$BD·AE,
∴7×4 = 5AE,解得AE = $\frac{28}{5}$。
∵AE⊥BD,AD⊥BC,
∴∠ACP = ∠BCD = ∠AED = 90°,
∴∠PAC + ∠APC = ∠PAC + ∠D,
∴∠APC = ∠D。又
∵AC = BC = 4,
∴△ACP≌△BCD(AAS),
∴AP = BD = 5,
∴PE = AE - AP = $\frac{28}{5}$ - 5 = $\frac{3}{5}$。故选B。
查看更多完整答案,请扫码查看


