2025年初中毕业升学真题详解八年级数学上册北师大版陕西专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年初中毕业升学真题详解八年级数学上册北师大版陕西专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第77页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
1. 化简$\sqrt{16}$ 的结果是(
A.-2
B.4
C.$\pm 4$
D.2
B
)。A.-2
B.4
C.$\pm 4$
D.2
答案:
1.B [点拨]本题考查算术平方根的定义,熟记概念是解题的关键。
[解析] $\sqrt{16}=4$。故选B。
[解析] $\sqrt{16}=4$。故选B。
2. 下列能说明命题“若$x$为无理数,则$x^2$也是无理数”是假命题的反例是(
A.$x = \sqrt{3} + 1$
B.$x = \sqrt{3} - 1$
C.$x = \sqrt{2}$
D.$x = \sqrt{3} - \sqrt{2}$
C
)。A.$x = \sqrt{3} + 1$
B.$x = \sqrt{3} - 1$
C.$x = \sqrt{2}$
D.$x = \sqrt{3} - \sqrt{2}$
答案:
2.C [点拨]本题考查命题与定理的知识,解题的关键是了解无理数的定义,难度不大。
[解析]当$x = \sqrt{2}$时,$x^{2} = (\sqrt{2})^{2} = 2$,满足$x$为无理数,但不满足$x^{2}$也是无理数。故选C。
[解析]当$x = \sqrt{2}$时,$x^{2} = (\sqrt{2})^{2} = 2$,满足$x$为无理数,但不满足$x^{2}$也是无理数。故选C。
3. 下列方程组中,是二元一次方程组的是(
A.$\begin{cases}x + 3y = 5, \\2x - 3z = 3\end{cases}$
B.$\begin{cases}m + n = 0, \frac{m}{6} + \frac{2n}{3} = 1\end{cases}$
C.$\begin{cases}m + n = 5, \\mn + n = 6\end{cases}$
D.$\begin{cases}3x + 2y = 10, \\x + \frac{2}{y} = 6\end{cases}$
B
)。A.$\begin{cases}x + 3y = 5, \\2x - 3z = 3\end{cases}$
B.$\begin{cases}m + n = 0, \frac{m}{6} + \frac{2n}{3} = 1\end{cases}$
C.$\begin{cases}m + n = 5, \\mn + n = 6\end{cases}$
D.$\begin{cases}3x + 2y = 10, \\x + \frac{2}{y} = 6\end{cases}$
答案:
3.B [点拨]本题考查二元一次方程组的定义。
[解析]A.方程组含有三个未知数,它不是二元一次方程组;
B.符合题意,它是二元一次方程组;C.$mn$项的次数为2,它不是二元一次方程组;D.存在不是整式的式子,它不是二元一次方程组。故选B。
[解析]A.方程组含有三个未知数,它不是二元一次方程组;
B.符合题意,它是二元一次方程组;C.$mn$项的次数为2,它不是二元一次方程组;D.存在不是整式的式子,它不是二元一次方程组。故选B。
4. 下列说法正确的是(
A.1 的平方根是 1
B.平方根是本身的数是 0 和 1
C.1 的立方根是 1
D.立方根是本身的数是 0 和 1
C
)。A.1 的平方根是 1
B.平方根是本身的数是 0 和 1
C.1 的立方根是 1
D.立方根是本身的数是 0 和 1
答案:
4.C [点拨]本题考查平方根和立方根的相关知识。
[解析]A.1的平方根是$\pm1$,故本选项错误;B.$\because$1的平方根是$\pm1$,0的平方根是0,$\therefore$平方根等于它本身的数只有0,故本选项错误;C.1的立方根是1,故本选项正确;D.1的立方根是1,0的立方根是0, - 1的立方根是 - 1,即立方根等于它本身的数是1,0, - 1,故本选项错误。故选C。
[解析]A.1的平方根是$\pm1$,故本选项错误;B.$\because$1的平方根是$\pm1$,0的平方根是0,$\therefore$平方根等于它本身的数只有0,故本选项错误;C.1的立方根是1,故本选项正确;D.1的立方根是1,0的立方根是0, - 1的立方根是 - 1,即立方根等于它本身的数是1,0, - 1,故本选项错误。故选C。
5. 一位同学把一副三角板在桌面上摆放成如图所示形状,若$DE // AB$,则$\angle 1$的度数为(
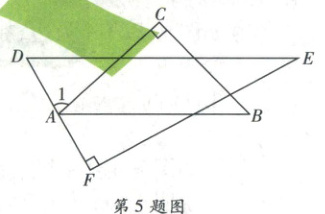
A.$95^{\circ}$
B.$85^{\circ}$
C.$75^{\circ}$
D.$65^{\circ}$
C
)。
A.$95^{\circ}$
B.$85^{\circ}$
C.$75^{\circ}$
D.$65^{\circ}$
答案:
5.C [点拨]本题考查平行线的性质,熟练掌握平行线的性质是解题的关键。
[解析] $\because DE// AB$,$\therefore\angle D=\angle BAF = 60^{\circ}$。
$\because\angle CAB = 45^{\circ}$,$\therefore\angle1 = 180^{\circ}-\angle BAF-\angle CAB = 75^{\circ}$。故选C。
[解析] $\because DE// AB$,$\therefore\angle D=\angle BAF = 60^{\circ}$。
$\because\angle CAB = 45^{\circ}$,$\therefore\angle1 = 180^{\circ}-\angle BAF-\angle CAB = 75^{\circ}$。故选C。
6. 已知$\begin{cases}x = 1, \\ y = -1\end{cases}$是方程组$\begin{cases}ax + by = 5, \\ bx - ay = 1\end{cases}$的解,则$(a + b)(a - b)$的值是( )。
A.5
B.-5
C.25
D.-25
A.5
B.-5
C.25
D.-25
答案:
6.A [点拨]本题考查二元一次方程组的解,代数式求值。
[解析]把$\begin{cases}x = 1\\y = -1\end{cases}$代入方程组$\begin{cases}ax + by = 5\\bx - ay = 1\end{cases}$中,得$\begin{cases}a - b = 5\\b + a = 1\end{cases}$
$\therefore(a + b)(a - b)=1×5 = 5$。故选A。
[解析]把$\begin{cases}x = 1\\y = -1\end{cases}$代入方程组$\begin{cases}ax + by = 5\\bx - ay = 1\end{cases}$中,得$\begin{cases}a - b = 5\\b + a = 1\end{cases}$
$\therefore(a + b)(a - b)=1×5 = 5$。故选A。
7. 已知某天五位同学体育锻炼的时间分别为(单位:小时):1,1.5,1.4,2,1.5,这组数据的中位数和众数分别是(
A.1.5,1.5
B.1.4,1.5
C.1.48,1.5
D.1,2
A
)。A.1.5,1.5
B.1.4,1.5
C.1.48,1.5
D.1,2
答案:
7.A [点拨]本题考查中位数和众数的概念。
[解析]这组数据按照从小到大的顺序排列为:1,1.4,1.5,1.5,2,则中位数是1.5,众数是1.5。故选A。
[解析]这组数据按照从小到大的顺序排列为:1,1.4,1.5,1.5,2,则中位数是1.5,众数是1.5。故选A。
8. 若直线$y = kx + b$经过第一、二、四象限,则函数$y = bx - k$的大致图象是(

B
)。
答案:
8.B [点拨]本题考查一次函数的图象和性质。
[解析] $\because$一次函数$y = kx + b$的图象经过第一、二、四象限,
$\therefore k<0$,$b>0$,$\therefore -k>0$,
$\therefore$一次函数$y = bx - k$的图象经过第一、二、三象限。故选B。
[解析] $\because$一次函数$y = kx + b$的图象经过第一、二、四象限,
$\therefore k<0$,$b>0$,$\therefore -k>0$,
$\therefore$一次函数$y = bx - k$的图象经过第一、二、三象限。故选B。
查看更多完整答案,请扫码查看


