《2025年初中毕业升学真题详解八年级数学上册北师大版陕西专版》

18. (4分)解方程。
(1)$\frac{1}{9}(x+2)^2=1$;
(2)$8(x-1)^3+27=0$。

答案： 18.[点拨]本题考查平方根和立方根的应用，熟练掌握立方根和平方根的定义是解题的关键。
[解析]
(1)$\frac{1}{9}(x+2)^2=1$，方程两边同乘9，得$(x+2)^2=9$，开平方，得$x+2=\pm3$，解得$x_1=1$，$x_2=-5$。
(2)$8(x-1)^3+27=0$，移项，得$8(x-1)^3=-27$，方程两边同除以8，得$(x-1)^3=-\frac{27}{8}$，开立方，得$x-1=-\frac{3}{2}$，解得$x=-\frac{1}{2}$。

19. (4分)如图,直线$l$垂直于数轴,请用尺规在数轴上作出表示$\sqrt{10}$的点$A$。(不写作法,保留作图痕迹)

答案：
19.[点拨]本题考查在数轴上找到表示无理数的点，利用勾股定理画出长度为$\sqrt{10}$的线段是解题的关键。
[解析]如图，点A即为所求。

20. 右侧扫码·视频讲解 (4分)已知$3a+4$的算术平方根是5,$5a-2b-2$的立方根是3,$c$是$\sqrt{29}-1$的整数部分,求$a+2b+3c$的平方根。

答案： 20.[点拨]本题考查估算无理数的大小，算术平方根、立方根，理解算术平方根、立方根的定义，掌握估算无理数的方法是正确解答的前提。
[解析]
∵$3a+4$的算术平方根是5，
∴$3a+4=5^2$，解得$a=7$。
∵$5a-2b-2$的立方根是3，
∴$5a-2b-2=3^3$，解得$b=3$。
∵$25＜29＜36$，
∴$5＜\sqrt{29}＜6$，
∴$4＜\sqrt{29}-1＜5$。
∵c是$\sqrt{29}-1$的整数部分，
∴$c=4$，
∴$a+2b+3c=7+2×3+3×4=25$。
∵25的平方根为$\pm5$，
∴$a+2b+3c$的平方根为$\pm5$。

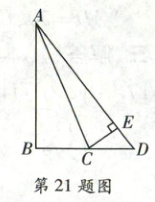
21. (6分)如图,在$\triangle ABC$中,$AC=13\ cm$,$AB=12\ cm$,$BC=5\ cm$,$D$是$BC$延长线上的点,连接$AD$,若$AD=15\ cm$。
(1)求$CD$的长;
(2)过点$C$作$CE\perp AD$于点$E$,求$CE$的长。

答案： 21.[点拨]本题考查勾股定理及其逆定理。
[解析]
(1)
∵$AC=13$cm，$AB=12$cm，$BC=5$cm，
∴$AC^2=169$，$AB^2=144$，$BC^2=25$，
∴$AC^2=AB^2+BC^2$，
∴$\triangle ABC$是直角三角形，且$\angle ABD=90°$。
在$Rt\triangle ABD$中，由勾股定理，
得$BD=\sqrt{AD^2-AB^2}=\sqrt{15^2-12^2}=9$(cm)，
∴$CD=BD-BC=9-5=4$(cm)。
(2)由
(1)得$CD=4$cm，$\angle ABD=90°$，
∴$AB\perp BD$。
∵$CE\perp AD$，
∴$S_{\triangle ACD}=\frac{1}{2}CD· AB=\frac{1}{2}AD· CE$，
∴$\frac{1}{2}×4×12=\frac{1}{2}×15CE$，解得$CE=\frac{16}{5}$，
∴$CE$的长为$\frac{16}{5}$cm。

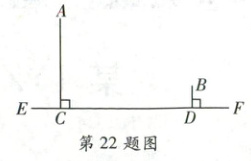
22. (6分)如图,在一条笔直的马路$EF$同侧有$A,B$两个小区,$A$小区到马路的垂直距离$AC$为10千米,$B$小区到马路的垂直距离$BD$为2千米,$CD$的长度为15千米。
(1)求$A,B$小区之间的距离;
(2)现要在$C,D$之间修建一个车站$G$,使得车站$G$到$A,B$两小区的距离相等,则车站$G$应修建在离点$C$多远处?

答案：
22.[点拨]本题考查勾股定理的应用，正确作出辅助线是解题的关键。
[解析]
(1)如图1，过点B作$BH\perp AC$于点H，则$\angle AHB=\angle BHC=90°$。
∵$\angle HCD=\angle CDB=90°$，
∴四边形CDBH是长方形，
∴$BH=CD=15$千米，$HC=BD=2$千米，
∴$AH=AC-HC=10-2=8$(千米)，
∴$AB=\sqrt{AH^2+BH^2}=\sqrt{8^2+15^2}=17$(千米)。
答：A，B小区之间的距离为17千米。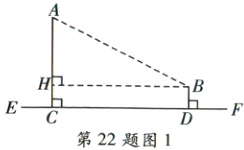
(2)如图2，设$CG=x$千米，则$DG=(15-x)$千米，
由题意，得$AG=BG$，
∴$10^2+x^2=2^2+(15-x)^2$，
整理得$30x=129$，解得$x=4.3$。
答：车站G应修建在离点C4.3千米处。