2025年初中毕业升学真题详解八年级数学上册北师大版陕西专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年初中毕业升学真题详解八年级数学上册北师大版陕西专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第72页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
22. 右侧扫码·视频讲解 ( 8 分) 如图, 已知一次函数 $y = \frac { 1 } { 2 } x + 2$ 的图象与 $x$ 轴交于点 $A$, 与 $y$ 轴交于点 $B$, 点 $C$ 与点 $A$ 关于 $y$ 轴对称。
( 1) 求 $\triangle AOB$ 的面积;
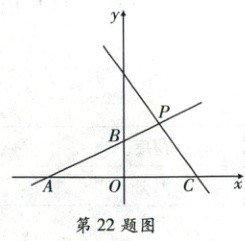
( 2) 若点 $P$ 在一次函数 $y = \frac { 1 } { 2 } x + 2$ 的图象上, 且在第一象限, $S _ { 四边形 O B P C } = \frac { 2 } { 3 } S _ { \triangle A P C }$, 求点 $P$ 的坐标。
( 1) 求 $\triangle AOB$ 的面积;

( 2) 若点 $P$ 在一次函数 $y = \frac { 1 } { 2 } x + 2$ 的图象上, 且在第一象限, $S _ { 四边形 O B P C } = \frac { 2 } { 3 } S _ { \triangle A P C }$, 求点 $P$ 的坐标。
答案:
22. [点拨]本题考查一次函数图象上点的坐标特征以及关于坐标轴对称的点的坐标特征。
[解析]
(1) $\because$在一次函数$y=\frac{1}{2}x + 2$中,当$x = 0$时,$y = 2$;
当$y = 0$时,$x = - 4$,
$\therefore A(-4,0)$,$B(0,2)$,
$\therefore S_{\triangle ABO}=\frac{1}{2}×4×2 = 4$。
(2) $\because$点C与点A关于y轴对称,$\therefore C(4,0)$,
如图,连接OP,
设点$P(m,\frac{1}{2}m + 2)(m > 0)$,
则$S_{四边形OBPC}=S_{\triangle BOP}+S_{\triangle POC}=\frac{1}{2}×2· m+\frac{1}{2}×4×(\frac{1}{2}m + 2)=2m + 4$,
$S_{\triangle APC}=\frac{1}{2}×8×(\frac{1}{2}m + 2)=2m + 8$,
$\because S_{四边形OBPC}=\frac{2}{3}S_{\triangle APC}$,
$\therefore2m + 4=\frac{2}{3}(2m + 8)$,解得$m = 2$,$\therefore P(2,3)$。

22. [点拨]本题考查一次函数图象上点的坐标特征以及关于坐标轴对称的点的坐标特征。
[解析]
(1) $\because$在一次函数$y=\frac{1}{2}x + 2$中,当$x = 0$时,$y = 2$;
当$y = 0$时,$x = - 4$,
$\therefore A(-4,0)$,$B(0,2)$,
$\therefore S_{\triangle ABO}=\frac{1}{2}×4×2 = 4$。
(2) $\because$点C与点A关于y轴对称,$\therefore C(4,0)$,
如图,连接OP,
设点$P(m,\frac{1}{2}m + 2)(m > 0)$,
则$S_{四边形OBPC}=S_{\triangle BOP}+S_{\triangle POC}=\frac{1}{2}×2· m+\frac{1}{2}×4×(\frac{1}{2}m + 2)=2m + 4$,
$S_{\triangle APC}=\frac{1}{2}×8×(\frac{1}{2}m + 2)=2m + 8$,
$\because S_{四边形OBPC}=\frac{2}{3}S_{\triangle APC}$,
$\therefore2m + 4=\frac{2}{3}(2m + 8)$,解得$m = 2$,$\therefore P(2,3)$。

23. 右侧扫码·视频讲解 ( 10 分) ( 1) 发现问题
如图 1, 已知在 $\triangle ABC$ 中, $AC = AB$, $\angle BAC = 30 ^ { \circ }$, $O$ 为 $\triangle ABC$ 内一点, 且 $OB = OC = BC$, 连接 $AO$, 则 $\angle AOC$ 的度数为
( 2) 探究问题
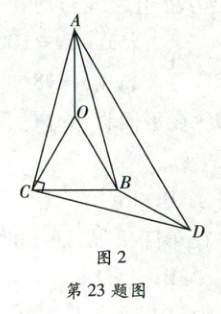
如图 2, 在( 1) 的条件下, 在 $AC$ 的右侧作 $CD \bot AC$, 垂足为 $C$, 且 $CD = CA$, 连接 $AD$, $BD$, 求 $\angle ABD$ 的度数;
( 3) 解决问题
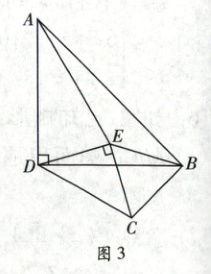
如图 3, 已知四边形 $ABCD$ 为某公园拟设计的一处休闲广场, $AD$, $BD$ 为两条主干道, 且 $DA = DB$, $AD \bot BD$, 设计人员计划在 $\triangle ABD$ 内确定一点 $E$, 满足以下条件: $AD = AE$, $\angle DAE = 30 ^ { \circ }$, $DE \bot CE$, $DE = CE$。 现准备在 $C$, $E$ 两处建造两个凉亭, $DE$, $EB$, $BC$, $CD$ 为休闲小道, 若 $DE = 60$ 米, 试求四边形 $BCDE$ 的面积。
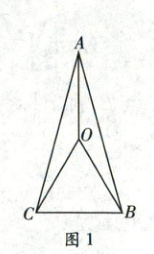
如图 1, 已知在 $\triangle ABC$ 中, $AC = AB$, $\angle BAC = 30 ^ { \circ }$, $O$ 为 $\triangle ABC$ 内一点, 且 $OB = OC = BC$, 连接 $AO$, 则 $\angle AOC$ 的度数为
150°
;( 2) 探究问题
如图 2, 在( 1) 的条件下, 在 $AC$ 的右侧作 $CD \bot AC$, 垂足为 $C$, 且 $CD = CA$, 连接 $AD$, $BD$, 求 $\angle ABD$ 的度数;
( 3) 解决问题
如图 3, 已知四边形 $ABCD$ 为某公园拟设计的一处休闲广场, $AD$, $BD$ 为两条主干道, 且 $DA = DB$, $AD \bot BD$, 设计人员计划在 $\triangle ABD$ 内确定一点 $E$, 满足以下条件: $AD = AE$, $\angle DAE = 30 ^ { \circ }$, $DE \bot CE$, $DE = CE$。 现准备在 $C$, $E$ 两处建造两个凉亭, $DE$, $EB$, $BC$, $CD$ 为休闲小道, 若 $DE = 60$ 米, 试求四边形 $BCDE$ 的面积。



答案:
23. [点拨]本题考查全等三角形的判定和性质、等边三角形的判定和性质等知识,解决问题的关键是根据题意正确作出辅助线。
[解析]
(1) $\because OB = OC = BC$,
$\therefore \angle OCB = 60^{\circ}$。
$\because AC = AB$,$\angle BAC = 30^{\circ}$,
$\therefore \angle ACB=\angle ABC = 75^{\circ}$,
$\therefore \angle ACO=\angle ACB-\angle OCB = 15^{\circ}$。
$\because OA = OA$,
$\therefore \triangle AOC\cong\triangle AOB(SSS)$,
$\therefore \angle CAO=\angle BAO=\frac{1}{2}\angle BAC = 15^{\circ}$,
$\therefore \angle AOC = 180^{\circ}-\angle CAO-\angle ACO = 180^{\circ}-15^{\circ}-15^{\circ}=150^{\circ}$。
故答案为$150^{\circ}$。
(2) $\because CD\bot AC$,
$\therefore \angle ACD = 90^{\circ}$,
由
(1)知,$\angle ACB = 75^{\circ}$,$\angle ACO = 15^{\circ}$,$OC = BC$,
$\therefore \angle DCB = 90^{\circ}-75^{\circ}=15^{\circ}$,
$\therefore \angle DCB=\angle ACO$。
$\because CD = CA$,
$\therefore \triangle BCD\cong\triangle OCA(SAS)$,
$\therefore \angle CBD=\angle AOC = 150^{\circ}$,
$\therefore \angle ABD = 360^{\circ}-\angle ABC-\angle CBD = 360^{\circ}-75^{\circ}-150^{\circ}=135^{\circ}$。
(3)如图,以DE为边在$\triangle ADE$内部作等边$\triangle DOE$,连接OA,
由
(1)
(2)知$OA = OD$,易证$\triangle BDE\cong\triangle ADO$,$\angle AEB = 135^{\circ}$,$\angle AED = 75^{\circ}$,
$\therefore BE = OA$,$DE = OD$,
$\therefore BE = DE$。
又$\because DE = CE$,
$\therefore BE = CE = DE = 60m$,
过点C作$CF\bot BE$于点F,则$\angle ECF = 30^{\circ}$,
$\therefore EF=\frac{1}{2}CE = 30m$,
则$CF=\sqrt{CE^{2}-EF^{2}} = 30\sqrt{3}(m)$,
$\therefore S_{\triangle BCE}=\frac{1}{2}BE· CF=\frac{1}{2}×60×30\sqrt{3}=900\sqrt{3}(m^{2})$,
$\because S_{\triangle CDE}=\frac{1}{2}DE^{2}=\frac{1}{2}×60^{2}=1800(m^{2})$,
$\therefore S_{四边形BCDE}=S_{\triangle BCE}+S_{\triangle CDE}=(900\sqrt{3}+1800)m^{2}$。

23. [点拨]本题考查全等三角形的判定和性质、等边三角形的判定和性质等知识,解决问题的关键是根据题意正确作出辅助线。
[解析]
(1) $\because OB = OC = BC$,
$\therefore \angle OCB = 60^{\circ}$。
$\because AC = AB$,$\angle BAC = 30^{\circ}$,
$\therefore \angle ACB=\angle ABC = 75^{\circ}$,
$\therefore \angle ACO=\angle ACB-\angle OCB = 15^{\circ}$。
$\because OA = OA$,
$\therefore \triangle AOC\cong\triangle AOB(SSS)$,
$\therefore \angle CAO=\angle BAO=\frac{1}{2}\angle BAC = 15^{\circ}$,
$\therefore \angle AOC = 180^{\circ}-\angle CAO-\angle ACO = 180^{\circ}-15^{\circ}-15^{\circ}=150^{\circ}$。
故答案为$150^{\circ}$。
(2) $\because CD\bot AC$,
$\therefore \angle ACD = 90^{\circ}$,
由
(1)知,$\angle ACB = 75^{\circ}$,$\angle ACO = 15^{\circ}$,$OC = BC$,
$\therefore \angle DCB = 90^{\circ}-75^{\circ}=15^{\circ}$,
$\therefore \angle DCB=\angle ACO$。
$\because CD = CA$,
$\therefore \triangle BCD\cong\triangle OCA(SAS)$,
$\therefore \angle CBD=\angle AOC = 150^{\circ}$,
$\therefore \angle ABD = 360^{\circ}-\angle ABC-\angle CBD = 360^{\circ}-75^{\circ}-150^{\circ}=135^{\circ}$。
(3)如图,以DE为边在$\triangle ADE$内部作等边$\triangle DOE$,连接OA,
由
(1)
(2)知$OA = OD$,易证$\triangle BDE\cong\triangle ADO$,$\angle AEB = 135^{\circ}$,$\angle AED = 75^{\circ}$,
$\therefore BE = OA$,$DE = OD$,
$\therefore BE = DE$。
又$\because DE = CE$,
$\therefore BE = CE = DE = 60m$,
过点C作$CF\bot BE$于点F,则$\angle ECF = 30^{\circ}$,
$\therefore EF=\frac{1}{2}CE = 30m$,
则$CF=\sqrt{CE^{2}-EF^{2}} = 30\sqrt{3}(m)$,
$\therefore S_{\triangle BCE}=\frac{1}{2}BE· CF=\frac{1}{2}×60×30\sqrt{3}=900\sqrt{3}(m^{2})$,
$\because S_{\triangle CDE}=\frac{1}{2}DE^{2}=\frac{1}{2}×60^{2}=1800(m^{2})$,
$\therefore S_{四边形BCDE}=S_{\triangle BCE}+S_{\triangle CDE}=(900\sqrt{3}+1800)m^{2}$。

查看更多完整答案,请扫码查看


