《2025年初中毕业升学真题详解八年级数学上册北师大版陕西专版》

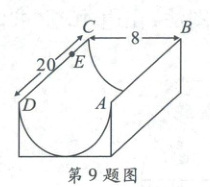
9. 右侧扫码·视频讲解 如图，这是一个供滑板爱好者使用的 U 型池的示意图，该 U 型池可以看作是长方体去掉一个“半圆柱”而成，中间可供滑行部分的截面是直径为$8\ m$的半圆，其边缘$AB = CD = 20\ m$，点$E$在$CD$上，$CE = 5\ m$，一名滑板爱好者从$A$点滑到$E$点，则他滑行的最短距离为(B)$ m$。(边缘部分的厚度可以忽略不计，$\pi$取$3$)

A.$17$
B.$3\sqrt{41}$
C.$4\sqrt{34}$
D.$25$

答案：
9. B [点拨]本题考查平面展开图，通过勾股定理解决最短路径问题。
[解析]将半圆柱展开可得如图所示的图形。$AD = \frac{\pi d}{2} = \frac{\pi}{2} × 8 = 12(米)$，$DE = DC - CE = 20 - 5 = 15(米)$。在$Rt\triangle ADE$中，$AE = \sqrt{AD^{2} + DE^{2}} = \sqrt{12^{2} + 15^{2}} = 3\sqrt{41}(米)$，即滑行的最短距离为$3\sqrt{41}$米。故选B。

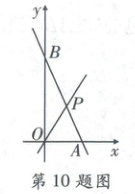
10. 右侧扫码·视频讲解 如图，一次函数$y = -3x + m$的图象与$x$轴、$y$轴的交点分别为$A$，$B$，直线$y = kx$与直线$AB$在第一象限的交点为$P$，若$\triangle BOP$与$\triangle AOP$的面积比为$\sqrt{3}$，则$k$的值为(C)。

A.$2\sqrt{3}$
B.$3$
C.$\sqrt{3}$
D.$2$

答案： 10. C [点拨]本题考查三角形的面积公式，正比例函数的性质。
[解析]如题图，过点$P$作$PC \perp x$轴于点$C$，$PD \perp y$轴于点$D$。由$y = -3x + m$可得$A(\frac{m}{3},0)$，$B(0,m)$，则$OA = \frac{m}{3}$，$OB = m$。设$P(x_1,y_1)$，则$\frac{1}{2}OB · PD = \sqrt{3} × \frac{1}{2}OA · PC$，即$y_1 = \sqrt{3}x_1$。又$\because$点$P$在$y = kx$上，$\therefore \sqrt{3}x_1 = kx_1$，$\therefore k = \sqrt{3}$。故选C。

11. 比较大小：$2\sqrt{3}$$＜$$\sqrt{13}$。（填“$＞$”“$=$”或“$＜$”）

答案： 11. $＜$ [点拨]本题考查二次根式的大小比较。
[解析] $\because 2\sqrt{3} = \sqrt{12}$，$\sqrt{12} ＜ \sqrt{13}$，$\therefore 2\sqrt{3} ＜ \sqrt{13}$。故答案为$＜$。

12. 校运动会上，八年级同学分别组建了红、黄、蓝三支仪仗队，各队队员身高($ cm$)的平均数$(\bar{x})$与方差$(s^2)$如表所示，则三支仪仗队中身高最整齐的是黄队。

答案： 12. 黄 [点拨]本题考查方差的意义。
[解析]由表知：黄队身高的方差最小，$\therefore$三支仪仗队中身高最整齐的是黄队。故答案为黄。

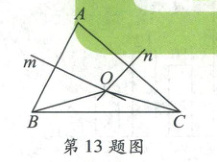
13. 如图，在$\triangle ABC$中，$AB$，$AC$的垂直平分线$m$，$n$相交于点$O$，若$\angle BAC = 72°$，则$\angle OBC$的度数为$18^{\circ}$。

答案： 13. $18^{\circ}$ [点拨]本题考查垂直平分线的性质及三角形的内角和。
[解析]如题图，连接$OA$。$\because$直线$m$，$n$分别为$AB$，$AC$的垂直平分线，$\therefore OA = OB$，$OA = OC$，$\therefore \angle OAB = \angle OBA$，$\angle OAC = \angle OCA$，$OB = OC$，即$\angle OBC = \angle OCB$。$\because \angle BAC = \angle OAB + \angle OAC = 72^{\circ}$，$\therefore \angle OBA + \angle OCA = 72^{\circ}$。$\because \angle ABC + \angle ACB + \angle BAC = 180^{\circ}$，$\therefore \angle OBC = \frac{1}{2} × (180^{\circ} - 72^{\circ} × 2) = 18^{\circ}$。故答案为$18^{\circ}$。

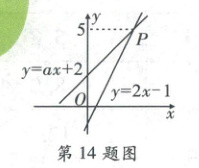
14. 如图，一次函数$y = ax + 2$与$y = 2x - 1$的图象相交于点$P$，则关于$x$的方程$ax + 2 = 2x - 1$的解是$x = 3$。

答案： 14. $x = 3$ [点拨]本题考查一元一次方程的解与一次函数图象交点坐标的关系。
[解析]根据题意，得点$P$的纵坐标为$5$，把$y = 5$代入$y = 2x - 1$，得$5 = 2x - 1$，解得$x = 3$。$\because$一次函数$y = ax + 2$与$y = 2x - 1$的图象相交于点$P$，$\therefore$关于$x$的方程$ax + 2 = 2x - 1$的解是$x = 3$。故答案为$x = 3$。

15. 右侧扫码·视频讲解 已知点$(-1, y_1)$，$(2, y_2)$在一次函数$y = (-k^2 - 3)x + 1$的图象上，则$y_1$$＞$$y_2$。(填“$＞$”“$=$”或“$＜$”)

答案： 15. $＞$ [点拨]本题考查一次函数的图象与性质。
[解析] $\because -k^{2} \leq 0$，$\therefore -k^{2} - 3 ＜ 0$，$\therefore$在$y = (-k^{2} - 3)x + 1$中，$y$随$x$的增大而减小。$\because -1 ＜ 2$，$\therefore y_1 ＞ y_2$。故答案为$＞$。

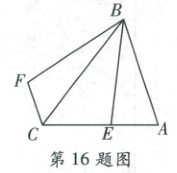
16. 右侧扫码·视频讲解 如图，在$\triangle ABC$中，$AB = AC$，$E$是边$AC$上一点，连接$BE$，在$BC$的左侧作$CF // AB$，且$CF = AE$，连接$BF$。若$AC = 10$，$BC = 12$，则四边形$EBFC$的面积为$48$。

答案：
16. $48$ [点拨]本题考查等腰三角形的性质，勾股定理。
[解析]如图，过点$B$作$BG \perp AC$于点$G$，$CH \perp AB$于点$H$。$\because S_{\triangle ABC} = \frac{1}{2}AB · CH = \frac{1}{2}AC · BG$且$AB = AC$，$\therefore CH = BG$。又$\because CF = AE$，$\therefore S_{\triangle BCF} = \frac{1}{2}CF · CH$，

$S_{\triangle ABE} = \frac{1}{2}AE · BG = S_{\triangle BCF}$，$\therefore S_{四边形EBFC} = S_{\triangle BCE} + S_{\triangle BCF} = S_{\triangle BCE} + S_{\triangle ABE} = S_{\triangle ABC}$。如图，过点$A$作$AM \perp BC$于点$M$，$\because AB = AC$且$AM \perp BC$，$\therefore BM = \frac{1}{2}BC = \frac{1}{2} × 12 = 6$，$\therefore AM = \sqrt{AB^{2} - BM^{2}} = \sqrt{10^{2} - 6^{2}} = 8$，$\therefore S_{四边形EBFC} = S_{\triangle ABC} = \frac{1}{2}BC · AM = \frac{1}{2} × 12 × 8 = 48$。故答案为$48$。

17. （9 分）
（1）计算：$-3^2 - \left(\dfrac{1}{2}\right)^{-2} + (\sqrt{9} - \pi)^0 - | - 2|$；
（2）计算：$\sqrt{48} ÷ \sqrt{3} + \sqrt{12} × \sqrt{\dfrac{1}{2}} - \sqrt{24}$；
（3）解二元一次方程组：$\begin{cases}5x - 2y = 17 \\ 3x + 4y = 5\end{cases}$。

答案： 17. [点拨]本题考查二次根式的运算，实数的混合运算，解二元一次方程组。
[解析]
(1)$-3^{2} - (\frac{1}{2})^{-2} + (\sqrt{9} - \pi)^{0} - | -2 | = -9 - 4 + 1 - 2 = -14$。
(2)$\sqrt{48} ÷ \sqrt{3} + \sqrt{12} × \sqrt{\frac{1}{2}} - \sqrt{24} = \sqrt{48 ÷ 3} + \sqrt{\frac{1}{2} × 12} - 2\sqrt{6} = 4 + \sqrt{6} - 2\sqrt{6} = 4 - \sqrt{6}$。
(3)$\begin{cases}5x - 2y = 17 & ①\\3x + 4y = 5 & ②\end{cases}$，$① × 2 + ②$，得$13x = 39$，解得$x = 3$。把$x = 3$代入$①$，得$y = -1$，$\therefore$方程组的解为$\begin{cases}x = 3\\y = -1\end{cases}$。