《2025年初中毕业升学真题详解八年级数学上册北师大版陕西专版》

11. 若$a$与$\sqrt{12}$是同类二次根式,请写出一个符合条件的最简二次根式$a$为$\boldsymbol{$$\sqrt{3}$$}$。

答案： 11.$\sqrt{3}$(答案不唯一) [点拨]本题考查同类二次根式,最简二次根式，掌握同类二次根式，最简二次根式的定义是关键。
[解析]根据题意可知，$\sqrt{12} = 2\sqrt{3}$与$a$是同类二次根式，$\therefore a$可以为$\sqrt{3}$。故答案为$\sqrt{3}$(答案不唯一)。

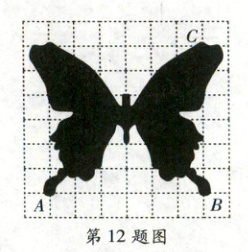
12. 如图,是一只蝴蝶标本,已知表示蝴蝶两“翅膀尾部”$A,B$两点的坐标分别为$(-3,-1)$,$(3,-1)$,则表示蝴蝶“翅膀顶端”点$C$的坐标为$\boldsymbol{$(3,5)$}$。

答案：
12.$(3,5)$ [点拨]本题考查坐标确定位置，理解点与坐标的关系是解题的关键。
[解析]$\because A$，$B$两点的坐标分别为$( - 3, - 1)$，$(3, - 1)$，则可得平面直角坐标系如图所示。

$\therefore$一个格代表$1$个单位长度，根据平移得点$C$的坐标为$(3,5)$。故答案为$(3,5)$。

13. 将直线$y = kx - 2$向左平移$2$个单位长度,再向下平移$6$个单位长度后,正好经过点$(2,4)$,则$k$的值为$\boldsymbol{$3$}$。

答案： 13.$3$ [点拨]本题考查一次函数图象的平移规律和用待定系数法求一次函数表达式，求出平移前经过的点是解题的关键。
[解析]$\because$直线平移后过点$(2,4)$，$\therefore$平移前经过点$(2 + 2,4 + 6)$，即点$(4,10)$。
将$(4,10)$代入$y = kx - 2$中，$10 = 4k - 2$，解得$k = 3$。故答案为$3$。

14. 如果某个二元一次方程组的解中两个未知数的值互为相反数,我们称这个方程组为“和谐方程组”。若关于$x,y$的方程组$\begin{cases}x + 3y = 4 + a,\\x - y = 3a\end{cases}$是“和谐方程组”,则$a$的值为$\boldsymbol{$ ______ $}$。

答案： 14.$ - 1$ [点拨]本题考查二元一次方程组的解，掌握整体法解方程组是解决此题的关键。
[解析]因为关于$x,y$的方程组$\begin{cases}x + 3y = 4 + a\\x - y = 3a\end{cases}$为“和谐方程组”，$\therefore x,y$互为相反数，①$ + $②，得$2x + 2y = 4 + 4a$，即$x + y = 2 + 2a$，所以$x + y = 2 + 2a = 0$，解得$a = - 1$。故答案为$- 1$。

15. 若一次函数$y = kx + 2k + 5$的图象不经过第一象限,则$k$的取值范围是$\boldsymbol{$k ≤ -5/2$}$。

答案： 15.$k \leq - \frac{5}{2}$ [点拨]本题考查一次函数图象与系数的关系,牢记“$k ＜ 0,b = 0 \Leftrightarrow y = kx + b$的图象在第二、四象限；$k ＜ 0,b ＜ 0 \Leftrightarrow y = kx + b$的图象在第二、三、四象限”是解题的关键。
[解析]当此函数的图象经过第二、四象限时，$\begin{cases}k ＜ 0\\2k + 5 = 0\end{cases}$，解得$k = - \frac{5}{2}$；当此函数的图象经过第二、三、四象限时，$\begin{cases}k ＜ 0\\2k + 5 ＜ 0\end{cases}$，解得$k ＜ - \frac{5}{2}$。综上所述，$k$的取值范围是$k \leq - \frac{5}{2}$。故答案为$k \leq - \frac{5}{2}$。

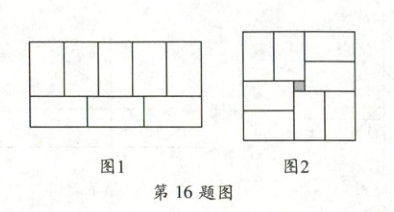
16. 右侧扫码·视频讲解 小明在拼图时,发现$8$个一样大小的长方形,恰好可以拼成一个大的长方形如图1;小红看见了,说:“我也来试一试。”结果小红七拼八凑,拼成了如图2那样的正方形,中间还留下了一个洞,恰好是面积为$25\ \mathrm{mm}^2$的小正方形,则每个小长方形的面积为$\boldsymbol{$375$}\ \mathrm{mm}^2$。

答案： 16.$375$ [点拨]本题考查二元一次方程的应用，找准等量关系，正确列出二元一次方程是解题的关键。
[解析]设每个小长方形的宽为$x mm$，长为$y mm$，根据题图1，题图2得$\begin{cases}3y = 5x\\2x - y = \sqrt{25}\end{cases}$，解得$\begin{cases}x = 15\\y = 25\end{cases}$，
$\therefore 25 × 15 = 375( mm^2)$，$\therefore$每个小长方形的面积为$375 mm^2$。故答案为$375$。

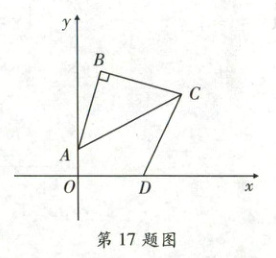
17. 右侧扫码·视频讲解 如图,在平面直角坐标系中,点$B(1,5)$,点$D(3,0)$,$A$为$y$轴上一点,连接$AB$,将$AB$绕点$B$逆时针旋转得$BC$,连接$AC$,得到等腰直角$\triangle ABC$,且$\angle ABC$为直角,连接$CD$,请写出当$|CB - CD|$最大时点$C$的坐标为$\boldsymbol{$(1/3,4)$}$。

答案：
17.$(\frac{1}{3},4)$ [点拨]本题考查一次函数的性质,轴对称的性质,全等三角形的判定与性质等知识，熟练掌握知识点的应用是解题的关键。
[解析]如图，过点$C$作直线$CH \perp y$轴于点$H$，过点$B$作$BE \perp y$轴于点$E$，作点$B$关于$CH$的对称点$B^{\prime}$，连接$BB^{\prime}$交$CH$于点$F$，

$\because \angle AEB = \angle CFB = 90^{\circ}$。
$\because \angle EHF = 90^{\circ}$，$\therefore \angle EBF = 90^{\circ}$。
由旋转性质可知，$AB = CB$，$\angle ABC = 90^{\circ}$，$\therefore \angle ABE = \angle CBF$，
在$\triangle ABE$和$\triangle CBF$中，$\begin{cases}\angle AEB = \angle CFB\\\angle ABE = \angle CBF\\AB = CB\end{cases}$
$\therefore \triangle ABE \cong \triangle CBF(AAS)$，$\therefore BE = BF$。
$\because$点$B(1,5)$，$\therefore BE = BF = 1$，则点$C$在$HF$上运动，$\therefore$点$C$的纵坐标为$4$，$\therefore B^{\prime}(1,3)$。$\because |B^{\prime}C - CD| \leq B^{\prime}D$，$\therefore$当$C,B^{\prime},D$三点共线时，$|B^{\prime}C - CD|$有最大值，即$|CB - CD|$有最大值，设直线$CD$解析式为$y = kx + b$。
$\because D(3,0)$，$B^{\prime}(1,3)$，$\therefore \begin{cases}3k + b = 0\\k + b = 3\end{cases}$，解得$\begin{cases}k = - \frac{3}{2}\\b = \frac{9}{2}\end{cases}$
$\therefore$直线$CD$解析式为$y = - \frac{3}{2}x + \frac{9}{2}$。
当$y = 4$时，$- \frac{3}{2}x + \frac{9}{2} = 4$，解得$x = \frac{1}{3}$，$\therefore C(\frac{1}{3},4)$。故答案为$(\frac{1}{3},4)$。

18. (8分)计算。
(1)$(\sqrt{2} - 3)^0 + \sqrt[3]{-27} + \sqrt{\dfrac{9}{2}}$;
(2)$\dfrac{\sqrt{48} - \sqrt{18}}{\sqrt{2}} + |1 - \sqrt{6}| - \sqrt{3} × 2\sqrt{8}$。

答案： 18.[点拨]本题考查实数的运算，零指数幂，掌握实数的运算法则是关键。
[解析]
(1)$(\sqrt{2} - 3)^{0} + \sqrt[3]{- 27} + \sqrt{\frac{9}{2}}$
$= 1 + ( - 3) + \frac{3\sqrt{2}}{2}$
$= - 2 + \frac{3\sqrt{2}}{2}$。
(2)$\frac{\sqrt{48} - \sqrt{18}}{\sqrt{2}} + |1 - \sqrt{6}| - \sqrt{3} × 2\sqrt{8}$
$= \sqrt{24} - 3 + \sqrt{6} - 1 - 2\sqrt{24}$
$= 2\sqrt{6} - 3 + \sqrt{6} - 1 - 4\sqrt{6}$
$= - \sqrt{6} - 4$。