《2025年初中毕业升学真题详解八年级数学上册北师大版陕西专版》

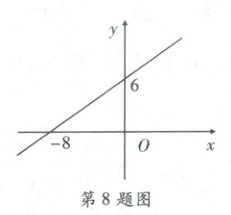
8. 一次函数$y = kx + b$($k,b$为常数且$kb \neq 0$)的图象如图所示,则关于$x$的方程$kx + b = 0$的解为(A)。

A.$x = -8$
B.$x = -6$
C.$x = 6$
D.$x = 8$

答案： 8.A [点拨]本题考查一次函数与一元一次方程，能正确根据一次函数的图象得出直线$y = kx + b$与$x$轴的交点坐标是解此题的关键。
[解析]从图象可知，直线$y = kx + b$与$x$轴的交点坐标是$(-8,0)$，所以关于$x$的方程$kx + b = 0$的解是$x = - 8$。故选A。

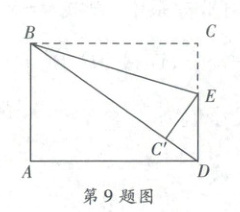
9. 右侧扫码·视频讲解 如图,已知长方形$ABCD$中,$AB = 9$,$AD = 12$,$E$是$CD$边上一点,将长方形沿直线$BE$折叠,使点$C$恰好落在对角线$BD$上的点$C'$处,则$BE$的长为(C)。

A.$5$
B.$13$
C.$4\sqrt{10}$
D.$15$
[视频讲解]

答案： 9.C [点拨]本题考查矩形的性质、翻折变换的性质、勾股定理等知识，正确地求出$C'D$的长是解题的关键。
[解析]$\because$四边形$ABCD$是矩形，$AB = 9$，$AD = 12$，$\therefore CD = AB = 9$，$BC = AD = 12$，$\angle C = 90^{\circ}$，$\therefore BD = \sqrt{CD^{2}+BC^{2}}=\sqrt{9^{2}+12^{2}} = 15$，由折叠得$C'E = CE$，$BC' = BC = 12$，$\angle BC'E = \angle C = 90^{\circ}$，$\therefore C'D = BD - BC' = 15 - 12 = 3$，$\angle DC'E = 90^{\circ}$，$\because C'D^{2}+C'E^{2}=DE^{2}$，且$DE = 9 - CE$，$\therefore 3^{2}+CE^{2}=(9 - CE)^{2}$，解得$CE = 4$，$\therefore BE = \sqrt{BC^{2}+CE^{2}}=\sqrt{12^{2}+4^{2}} = 4\sqrt{10}$。故选C。

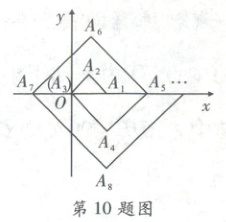
10. 右侧扫码·视频讲解 如图,$\triangle A_1A_2A_3$,$\triangle A_3A_4A_5$,$\triangle A_5A_6A_7$,$·s$,都是斜边在$x$轴上、斜边长分别为$2,4,6,·s$的等腰直角三角形,若$\triangle A_1A_2A_3$的顶点坐标分别为$A_1(2,0)$,$A_2(1,1)$,$A_3(0,0)$,则依图中所示规律,$A_{2023}$的坐标为(C)。

A.$(1012,0)$
B.$(-1008,0)$
C.$(-1010,0)$
D.$(-1012,0)$
[视频讲解]

答案： 10.C [点拨]本题考查点的坐标规律，找到变化规律是解题的关键。
[解析]$\because A_{1}(2,0)$，$A_{3}(0,0)$，$A_{5}(4,0)$，$A_{7}(-2,0)$，$A_{9}(6,0)$，$A_{11}(-4,0)$，$·s$，可得$n$为奇数时，$x_{A_{n}}=2 × (1 - 1 + 2 - 3 + 4 - 5 + 6 - 7 + ·s \pm \frac{n - 1}{2})$，当$\frac{n - 1}{2}$为奇数前面是减，当$\frac{n - 1}{2}$为偶数前面是加，$(2023 - 1) ÷ 2 = 1011$，$\therefore x_{A_{2023}}=2 × (1 - 1 + 2 - 3 + 4 - 5 + 6 - 7 + ·s + 1010 - 1011)= - 1010$，$\therefore A_{2023}$的坐标为$(- - 1010,0)$。故选C。

11. 若二次根式$\sqrt{a - 2}$有意义,则$a$的取值范围是$a \geqslant 2$。

答案： 11.$a \geqslant 2$ [点拨]本题考查二次根式有意义的条件，熟记二次根式的被开方数是非负数是解题的关键。
[解析]由题意得，$a - 2 \geqslant 0$，解得$a \geqslant 2$。故答案为$a \geqslant 2$。

12. 将直线$y = 2x$向上平移$1$个单位长度,得到一个一次函数的图象,所得一次函数的表达式是$y = 2x + 1$。

答案： 12.$y = 2x + 1$ [点拨]本题考查一次函数图象与几何变换，熟练掌握掌握一次函数图象的平移规律是解题的关键，左加右减，上加下减。
[解析]根据题意，$y = 2x$向上平移$1$个单位长度，平移后的直线表达式为$y = 2x + 1$。故答案为$y = 2x + 1$。

13. 若点$P(-1,y_1)$和点$Q(3,y_2)$是一次函数$y = -2x + 3$的图象上的两点,$y_1$与$y_2$的大小关系是:$y_1$$＞$$y_2$(填“$＞$”“$＜$”或“$=$”)。

答案： 13.$＞$ [点拨]本题考查一次函数的性质，牢记$k＞0$，$y$随$x$的增大而增大;$k＜0$，$y$随$x$的增大而减小”是解题的关键。
[解析]$\because k = - 2＜0$，$\therefore y$随$x$的增大而减小。又$\because$点$P(-1,y_{1})$和点$Q(3,y_{2})$是一次函数$y = - 2x + 3$的图象上的两点，且$-1＜3$，$\therefore y_{1}＞y_{2}$。故答案为$＞$。

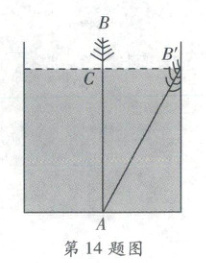
14. 古代著作《九章算术》中有一道“引葭赴岸”问题:今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,水深几何? 如图,其大意是:有一个池塘,其底面是边长为$10$尺的正方形,一棵芦苇$AB$生长在它的中央,高出水面部分$BC$为$1$尺。如果把芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部恰好碰到岸边,则水深为12尺。

答案： 14.12 [点拨]本题考查勾股定理的应用，熟记勾股定理是解题的关键。
[解析]由题意得，$CB' = 5$尺，设$AC = x$尺，则$AB'=(x + 1)$尺，$\because AC^{2}+CB'^{2}=AB'^{2}$，$\therefore x^{2}+5^{2}=(x + 1)^{2}$，解得$x = 12$。故答案为$12$。