2025年初中毕业升学真题详解八年级数学上册北师大版陕西专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年初中毕业升学真题详解八年级数学上册北师大版陕西专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第24页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
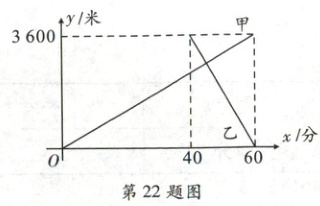
22. 右侧扫码·视频讲解 (7 分)已知$A,B$两地相距$3600$米,甲从$A$地出发步行到$B$地,$40$分钟后乙从$B$地出发骑自行车到$A$地,设甲步行的时间为$x$分钟,甲、乙两人离$A$地的距离分别为$y_1$米、$y_2$米,$y_1,y_2$与$x$的函数关系图象如图所示,根据图象解答下列问题:
(1) 求$y_1,y_2$与$x$的函数关系式;
(2) 求甲出发后多少分钟两人相遇,相遇时乙离$A$地多少米?
(1) 求$y_1,y_2$与$x$的函数关系式;
(2) 求甲出发后多少分钟两人相遇,相遇时乙离$A$地多少米?

答案:
22. [点拨]本题考查一次函数的应用,解题的关键是读懂题意,能从函数图象中获取有用的信息。
[解析]
(1)甲的速度为$3600 ÷ 60 = 60( 米/分)$,
$\therefore y_1 = 60x(0 \leq x \leq 60)$,
乙的速度为$3600 ÷ (60 - 40) = 180( 米/分)$,
$\therefore y_2 = 3600 - 180(x - 40) = -180x + 10800(40 \leq x \leq 60)$。
(2)两人相遇时距$A$地距离相等,
$\therefore 60x = -180x + 10800$,解得$x = 45$,
此时$-180x + 10800 = -180 × 45 + 10800 = 2700$,
$\therefore$甲出发后$45$分钟两人相遇,相遇时乙离$A$地$2700$米。
[解析]
(1)甲的速度为$3600 ÷ 60 = 60( 米/分)$,
$\therefore y_1 = 60x(0 \leq x \leq 60)$,
乙的速度为$3600 ÷ (60 - 40) = 180( 米/分)$,
$\therefore y_2 = 3600 - 180(x - 40) = -180x + 10800(40 \leq x \leq 60)$。
(2)两人相遇时距$A$地距离相等,
$\therefore 60x = -180x + 10800$,解得$x = 45$,
此时$-180x + 10800 = -180 × 45 + 10800 = 2700$,
$\therefore$甲出发后$45$分钟两人相遇,相遇时乙离$A$地$2700$米。
23. 右侧扫码·视频讲解 (10 分)小莉同学在一次数学练习中曾经遇到了平面直角坐标系中的折叠问题,张老师讲评完试卷后又让她尝试完成以下同类问题:
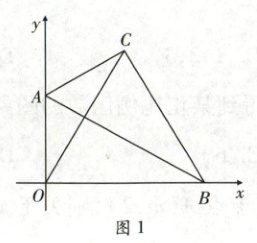
(1) 如图 1,在平面直角坐标系中,$A(0,2\sqrt{3})$,$B$分别是坐标轴上的两点,当$\angle ABO = 30°$时,将$\triangle AOB$沿边$AB$翻折得到$\triangle ACB$,点$O$的对应点为$C$,则点$C$坐标为
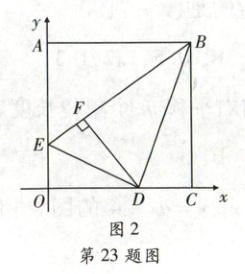
(2) 如图 2,长方形$OABC$位于平面直角坐标系中,点$A(0,17)$,$C(16,0)$,$E(0,5)$分别位于两个坐标轴上,$D$是$OC$上一动点,将$\mathrm{Rt}\triangle ODE$沿$DE$翻折得到$\triangle FDE$,当点$F$落在$BE$上时,试求$BD$所在直线的函数表达式;
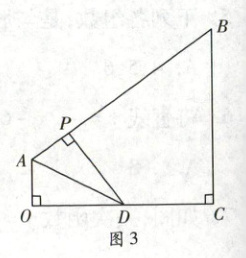
(3) 如图 3,四边形$OABC$是工厂张师傅设计的某零件平面示意图的一部分,$P,D$分别是$AB,OC$上两点,且$\angle AOD = \angle APD = \angle OCB = 90°$,$OA = AP = 2\ \mathrm{dm}$,$OC = BC = 8\ \mathrm{dm}$,现准备在$BC$边上再确定一点$Q$,画出一条分割线$PQ$,使得$S_{\triangle BPQ} = \frac{3}{5}S_{ 四边形ABCD}$,若存在点$Q$,请求出$BQ$的长度,若不存在,请说明理由。
(1) 如图 1,在平面直角坐标系中,$A(0,2\sqrt{3})$,$B$分别是坐标轴上的两点,当$\angle ABO = 30°$时,将$\triangle AOB$沿边$AB$翻折得到$\triangle ACB$,点$O$的对应点为$C$,则点$C$坐标为
$(3,3\sqrt{3})$
;(2) 如图 2,长方形$OABC$位于平面直角坐标系中,点$A(0,17)$,$C(16,0)$,$E(0,5)$分别位于两个坐标轴上,$D$是$OC$上一动点,将$\mathrm{Rt}\triangle ODE$沿$DE$翻折得到$\triangle FDE$,当点$F$落在$BE$上时,试求$BD$所在直线的函数表达式;
(3) 如图 3,四边形$OABC$是工厂张师傅设计的某零件平面示意图的一部分,$P,D$分别是$AB,OC$上两点,且$\angle AOD = \angle APD = \angle OCB = 90°$,$OA = AP = 2\ \mathrm{dm}$,$OC = BC = 8\ \mathrm{dm}$,现准备在$BC$边上再确定一点$Q$,画出一条分割线$PQ$,使得$S_{\triangle BPQ} = \frac{3}{5}S_{ 四边形ABCD}$,若存在点$Q$,请求出$BQ$的长度,若不存在,请说明理由。



答案:
23. [点拨]本题考查一次函数的综合运用,涉及三角形全等、面积的计算、图象的翻折等,正确作出辅助线是解题的关键。
[解析]
(1)在$ Rt \triangle ABO$中,$AO = 2\sqrt{3}$,$\angle ABO = 30^{\circ}$,
则$AB = 4\sqrt{3}$,则$OB = \sqrt{AB^{2} - OA^{2}} = 6$。
由图象的翻折知,$BO = BC = 6$,$\angle OBC = 2\angle ABO = 60^{\circ}$,
则$\triangle BOC$为等边三角形。
如图1,过点$C$作$CH \perp OB$,则$OH = HB = \frac{1}{2}OB = 3$,
则$CH = \sqrt{BC^{2} - BH^{2}} = 3\sqrt{3}$。
故点$C(3,3\sqrt{3})$。
(2)$\because AE = OA - OE = 17 - 5 = 12$,$OC = AB = 16$,
则$BE = \sqrt{AE^{2} + AB^{2}} = 20$。
由图象的翻折知,$OE = EF = 5$,则$BF = BE - EF = 20 - 5 = 15$。
设$FD = x = OD$,则$CD = 16 - x$,
则$BD^{2} = CB^{2} + CD^{2} = BF^{2} + FD^{2}$,
即$15^{2} + x^{2} = 17^{2} + (16 - x)^{2}$,
解得$x = 10$,即点$D(10,0)$。
$\because$点$B(16,17)$,
则由点$B,D$的坐标得,直线$BD$的表达式为$y = \frac{17}{6}x - \frac{85}{3}$。
(3)存在,理由如下:
建立如图2所示的平面直角坐标系,过点$B$作$BM \perp y$轴于点$M$,过点$P$作$PN \perp BC$于点$N$,连接$BD$。
在$ Rt \triangle ABM$中,$BM = CO = 8$,$AM = 8 - 2 = 6$,则$AB = 10$,
则$BP = AB - AP = 8 - AP$,$CB = 10$。
$\because BD = BD$,$\therefore Rt \triangle BDP \cong Rt \triangle BDC( HL)$。
又$\because AP = AO$,$AD = AD$,
$\therefore Rt \triangle APD \cong Rt \triangle AOD( HL)$。
则$PD = CD = OD = \frac{1}{2}OC = 4$,则点$D(4,0)$。
由点$A(0,2)$,$B(8,8)$,得直线$AB$的表达式为$y = \frac{3}{4}x + 2$。
设点$P(m,\frac{3}{4}m + 2)$,
由$PD = 4$得$(4 - m)^{2} + (\frac{3}{4}m + 2)^{2} = 4^{2}$,
解得$m = \frac{8}{5}$,则$PN = 8 - m = \frac{32}{5}$。
$\because S_{\triangle BPQ} = \frac{3}{5}S_{ 四边形ABCD}$,
而$S_{ 四边形ABCD} = S_{ 梯形AOCB} - S_{\triangle AOD} = \frac{1}{2} × (2 + 8) × 8 - \frac{1}{2} × 2 × 4$,
$\therefore \frac{1}{2}BQ · PN = \frac{3}{5} × [\frac{1}{2} × (2 + 8) × 8 - \frac{1}{2} × 2 × 4]$,
即$\frac{1}{2} × (2 + 8) × 8 - \frac{1}{2} × 2 × 4 = \frac{5}{3} × \frac{1}{2} · BQ · \frac{32}{5}$,
解得$BQ = \frac{27}{4}$,$\therefore BQ$的长度为$\frac{27}{4} dm$。


23. [点拨]本题考查一次函数的综合运用,涉及三角形全等、面积的计算、图象的翻折等,正确作出辅助线是解题的关键。
[解析]
(1)在$ Rt \triangle ABO$中,$AO = 2\sqrt{3}$,$\angle ABO = 30^{\circ}$,
则$AB = 4\sqrt{3}$,则$OB = \sqrt{AB^{2} - OA^{2}} = 6$。
由图象的翻折知,$BO = BC = 6$,$\angle OBC = 2\angle ABO = 60^{\circ}$,
则$\triangle BOC$为等边三角形。
如图1,过点$C$作$CH \perp OB$,则$OH = HB = \frac{1}{2}OB = 3$,
则$CH = \sqrt{BC^{2} - BH^{2}} = 3\sqrt{3}$。
故点$C(3,3\sqrt{3})$。
(2)$\because AE = OA - OE = 17 - 5 = 12$,$OC = AB = 16$,
则$BE = \sqrt{AE^{2} + AB^{2}} = 20$。
由图象的翻折知,$OE = EF = 5$,则$BF = BE - EF = 20 - 5 = 15$。
设$FD = x = OD$,则$CD = 16 - x$,
则$BD^{2} = CB^{2} + CD^{2} = BF^{2} + FD^{2}$,
即$15^{2} + x^{2} = 17^{2} + (16 - x)^{2}$,
解得$x = 10$,即点$D(10,0)$。
$\because$点$B(16,17)$,
则由点$B,D$的坐标得,直线$BD$的表达式为$y = \frac{17}{6}x - \frac{85}{3}$。
(3)存在,理由如下:
建立如图2所示的平面直角坐标系,过点$B$作$BM \perp y$轴于点$M$,过点$P$作$PN \perp BC$于点$N$,连接$BD$。
在$ Rt \triangle ABM$中,$BM = CO = 8$,$AM = 8 - 2 = 6$,则$AB = 10$,
则$BP = AB - AP = 8 - AP$,$CB = 10$。
$\because BD = BD$,$\therefore Rt \triangle BDP \cong Rt \triangle BDC( HL)$。
又$\because AP = AO$,$AD = AD$,
$\therefore Rt \triangle APD \cong Rt \triangle AOD( HL)$。
则$PD = CD = OD = \frac{1}{2}OC = 4$,则点$D(4,0)$。
由点$A(0,2)$,$B(8,8)$,得直线$AB$的表达式为$y = \frac{3}{4}x + 2$。
设点$P(m,\frac{3}{4}m + 2)$,
由$PD = 4$得$(4 - m)^{2} + (\frac{3}{4}m + 2)^{2} = 4^{2}$,
解得$m = \frac{8}{5}$,则$PN = 8 - m = \frac{32}{5}$。
$\because S_{\triangle BPQ} = \frac{3}{5}S_{ 四边形ABCD}$,
而$S_{ 四边形ABCD} = S_{ 梯形AOCB} - S_{\triangle AOD} = \frac{1}{2} × (2 + 8) × 8 - \frac{1}{2} × 2 × 4$,
$\therefore \frac{1}{2}BQ · PN = \frac{3}{5} × [\frac{1}{2} × (2 + 8) × 8 - \frac{1}{2} × 2 × 4]$,
即$\frac{1}{2} × (2 + 8) × 8 - \frac{1}{2} × 2 × 4 = \frac{5}{3} × \frac{1}{2} · BQ · \frac{32}{5}$,
解得$BQ = \frac{27}{4}$,$\therefore BQ$的长度为$\frac{27}{4} dm$。


查看更多完整答案,请扫码查看


