《2025年初中毕业升学真题详解八年级数学上册北师大版陕西专版》

22. 右侧扫码·视频讲解 (8分)某公司要印制新产品宣传材料。甲印刷厂提出:每份材料收1元印制费,另收1500元制版费;乙印刷厂提出:每份材料收2.5元印制费,不收制版费。图中$l_1$,$l_2$分别表示两家印刷厂的收费$y$(元)与印制数量$x$(份)之间的关系。
(1) 表示甲厂收费与印制数量之间关系的直线是l₁;(填“$l_1$”或“$l_2$”)
(2) 分别求出甲、乙两厂的收费$y$(元)与印制数量$x$(份)之间的解析式;
(3) 某厂商拟拿出3000元用于印制宣传材料,找哪家印刷厂印制宣传材料能多一些? 能多印多少份?

答案： 22. [点拨]本题考查求一次函数的解析式及一次函数的实际应用。
[解析]
(1)
∵甲印刷厂提出：每份材料收1元印制费，另收1500元制版费，
∴当x = 0时，y = 1500。故直线l₁表示甲厂收费与印制数量之间的关系。故答案为l₁。
(2)设l₁的解析式为y甲 = k₁x + b(x ≥ 0，且x取整数)，l₂的解析式为y乙 = k₂x(x ≥ 0，且x取整数)。
将点(0,1500)，(1000,2500)代入y甲 = k₁x + b，
得$\begin{cases}b = 1500 \\1000k₁ + b = 2500 \end{cases}$，解得$\begin{cases}k₁ = 1 \\b = 1500 \end{cases}$，
∴y甲 = x + 1500(x ≥ 0，且x取整数)。
将(1000,2500)代入y乙 = k₂x，得1000k₂ = 2500，解得k₂ = 2.5，
∴y乙 = 2.5x(x ≥ 0，且x取整数)。
(3)当y甲 = 3000时，x + 1500 = 3000，解得x = 1500；
当y乙 = 3000时，2.5x = 3000，解得x = 1200。
∵1500 ＞ 1200，1500 - 1200 = 300(份)，
∴拿出3000元用于印制宣传材料，找甲印刷厂印制宣传材料能多一些，能多印300份。

23. 右侧扫码·视频讲解 (10分)【问题发现】
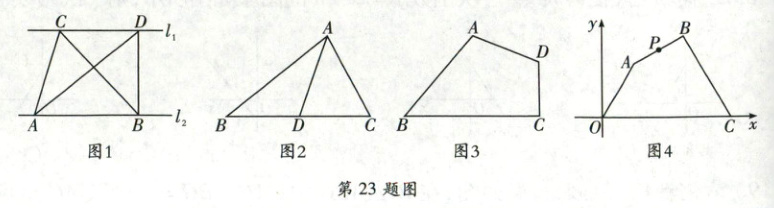
小明和小亮两位同学在研究三角形面积转换时发现:如图1,若直线$l_1 // l_2$,则$S_{\triangle ABC} = S_{\triangle ABD}$。
【问题探究】
(1) 如图2,$\triangle ABC$中,$D$为$BC$的中点,连接$AD$,则$S_{\triangle ABD}$=$S_{\triangle ACD}$(填“$=$”或“$\neq$”)
(2) 如图3,已知四边形$ABCD$,请画图在射线$BC$上找出一点$E$,使$S_{ 四边形ABCD}$与$S_{\triangle ABE}$相等,并说明理由;
【问题解决】
(3) 如图4,在平面直角坐标系中,有四边形$OABC$,点$A,B$在第一象限,点$C$的坐标为$(8,0)$,$\angle AOC = \angle BCO = 60°$,$OA = 4$,$BC = 6$,$P$为$AB$的中点,是否存在过点$P$的一条直线将四边形$OABC$的面积平分? 若存在,求出直线的解析式;若不存在,请说明理由。

答案：
23. [点拨]本题考查三角形中线的性质，坐标与图形，求一次函数解析式，勾股定理，含30°角的直角三角形的性质，中点坐标公式，熟练掌握待定系数法是解题的关键。
[解析]
(1)
∵△ABC中，D为BC的中点，
∴AD为BC边上的中线，
∴S△ABD = S△ACD。故答案为 =。
(2)如图1，连接AC，过点D作DE // AC，交射线BC于点E，连接AE，则点E即为所求作的点。理由如下：
∵DE // AC，
∴S△ACD = S△ACE，
∴S△ABE = S△ABC + S△ACE = S△ABC + S△ACD = S四边形ABCD


(3)存在。理由如下：
如图2，过点A作AD⊥x轴于点D，过点B作BE⊥x轴于点E，在OC上取点Q，使$\frac{OQ}{CQ}$ = $\frac{3}{2}$，连接AQ，BQ，作直线PQ，则∠ADO = ∠BEC = 90°。
∵∠AOC = ∠BCO = 60°，
∴∠OAD = ∠CBE = 90° - 60° = 30°，
∴OD = $\frac{1}{2}$AO = 2，CE = $\frac{1}{2}$BC = 3，
∴AD = $\sqrt{OA^{2} - OD^{2}}$ = 2$\sqrt{3}$，BE = $\sqrt{BC^{2} - CE^{2}}$ = 3$\sqrt{3}$。
∵C(8,0)，
∴OC = 8。
∵$\frac{OQ}{CQ}$ = $\frac{3}{2}$，
∴OQ = $\frac{3}{5}$×8 = $\frac{24}{5}$，CQ = $\frac{2}{5}$×8 = $\frac{16}{5}$，
∴S△AOQ = $\frac{1}{2}$OQ·AD = $\frac{1}{2}$×$\frac{24}{5}$×2$\sqrt{3}$ = $\frac{24\sqrt{3}}{5}$，
S△BCQ = $\frac{1}{2}$CQ·BE = $\frac{1}{2}$×$\frac{16}{5}$×3$\sqrt{3}$ = $\frac{24\sqrt{3}}{5}$，
∴S△AOQ = S△BCQ。
∵P为AB的中点，
∴S△APQ = S△BPQ，
∴S△AOQ + S△APQ = S△BCQ + S△BPQ，
∴直线PQ将四边形OABC分成面积相等的两部分。
∵AD = 2$\sqrt{3}$，BE = 3$\sqrt{3}$，OD = 2，OE = OC - CE = 8 - 3 = 5，
∴A(2,2$\sqrt{3}$)，B(5,3$\sqrt{3}$)，
∴P($\frac{2 + 5}{2}$,$\frac{2\sqrt{3} + 3\sqrt{3}}{2}$)，即P($\frac{7}{2}$,$\frac{5\sqrt{3}}{2}$)。
设直线PQ的解析式为y = kx + b，
把P($\frac{7}{2}$,$\frac{5\sqrt{3}}{2}$)，Q($\frac{24}{5}$,0)代入，得$\begin{cases}\frac{7}{2}k + b = \frac{5\sqrt{3}}{2} \frac{24}{5}k + b = 0 \end{cases}$，
解得$\begin{cases}k = - \frac{25\sqrt{3}}{13} \\b = \frac{120\sqrt{3}}{13} \end{cases}$，
∴直线PQ的解析式为y = - $\frac{25\sqrt{3}}{13}$x + $\frac{120\sqrt{3}}{13}$。