《2025年初中毕业升学真题详解八年级数学上册北师大版陕西专版》

22. 右侧扫码·视频讲解 (12分)某汽车销售公司计划购进一批新能源汽车尝试进行销售，据了解，2辆A型新能源汽车，1辆B型新能源汽车的进价共计50万元;3辆A型新能源汽车，2辆B型新能源汽车的进价共计85万元。
(1)求A，B两种型号的新能源汽车每辆的进价分别为多少万元;
(2)若该公司计划正好用220万元购进以上两种型号的新能源汽车(两种型号的新能源汽车均购买)，请你通过计算帮该公司求出全部的购买方案。

答案： 22. [点拨]本题考查二元一次方程组的应用及方程的整数解问题。
[解析]
(1) 设每辆A型汽车的进价为x万元，每辆B型汽车的进价为y万元，
依据题意可得$\begin{cases}2x + y = 50 \\3x + 2y = 85\end{cases}$，解得$\begin{cases}x = 15 \\y = 20\end{cases}$
答：每辆A型汽车的进价为15万元，每辆B型汽车的进价为20万元。
(2) 设购进m辆A型汽车，n辆B型汽车，
依题意得15m + 20n = 220，
∴m = $\frac{220 - 20n}{15}$ = $\frac{44 - 4n}{3}$。
又
∵m，n均为正整数，
∴$\begin{cases}m = 4 \\n = 8\end{cases}$，$\begin{cases}m = 8 \\n = 5\end{cases}$，$\begin{cases}m = 12 \\n = 2\end{cases}$
∴该公司共有3种购买方案，
方案1: 购进4辆A型汽车，8辆B型汽车；
方案2: 购进8辆A型汽车，5辆B型汽车；
方案3: 购进12辆A型汽车，2辆B型汽车。

23. 右侧扫码·视频讲解 (12分)在平面直角坐标系中，如果一个点到两坐标轴的距离相等，那么这个点称为“等距点”，例如(1,1)，(2,-2)，(-3,-3)，(4,-4)都称为“等距点”。
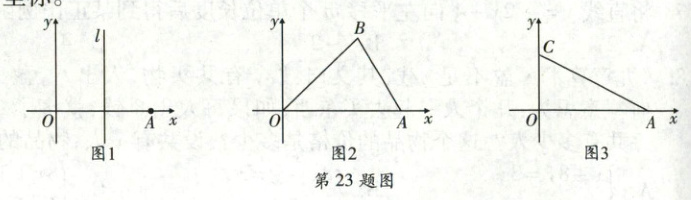
(1)如图1，点A(6,0)，线段OA的垂直平分线l上在第一象限内的“等距点”P的坐标为(3,3);视频讲解
(2)如图2，点A(6,0)，点B是第一象限内的“等距点”(4,4)，若点Q是第四象限内的“等距点”，是否存在点Q，使直线QB把$\triangle OBA$分成面积之比为1:2的两部分?若存在，请求出Q点坐标;若不存在，请说明理由。
(3)如图3，点A(6,0)，点C(0,3)，点D是坐标系内与原点O不重合的“等距点”，连接CD，AD，当$\angle CDA = 90^{\circ}$时，求“等距点”D的坐标。

答案：
23. [点拨]本题考查新定义，坐标与图形，全等三角形的判定与性质，一次函数的应用，要注意数形结合。
[解析]
(1)
∵点A(6,0)，
∴线段OA的垂直平分线l上在第一象限内的“等距点”P的坐标为(3,3)。故答案为(3,3)。
(2) 存在，理由如下：
如题图2，设BQ交OA于点P，
∵BQ将△OBA的面积分为1:2的两部分，
∴点P经过P₁(2,0)或P₂(4,0)。
∵点Q在第四象限，
∴点Q在直线y = - x上，
①当BQ经过P₁(2,0)时，y$_{BQ}$ = 2x - 4，
联立$\begin{cases}y_{BQ} = 2x - 4 \\y = - x\end{cases}$，解得$\begin{cases}x = \frac{4}{3} \\y = - \frac{4}{3}\end{cases}$
∴点Q的坐标为($\frac{4}{3}$， - $\frac{4}{3}$)；
②当BQ经过P₂(4,0)时，点Q在直线x = 4上，
联立$\begin{cases}x = 4 \\y = - x\end{cases}$，解得$\begin{cases}x = 4 \\y = - 4\end{cases}$
∴点Q的坐标为(4, - 4)，
综上，点Q的坐标为($\frac{4}{3}$， - $\frac{4}{3}$)或(4, - 4)。
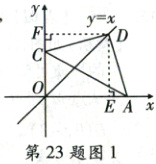
(3) ①如图1，当点D在直线y = x上时，过点D作DE⊥x轴，DF⊥y轴，则∠CFD = ∠DEA = 90°，
∵∠CDE + ∠CDF = ∠CDE + ∠EDA = 90°，
∴∠CDF = ∠EDA。
∵D是“等距点”，
∴DF = DE，
∴△CFD≌△AED，
∴CF = AE，
设点D(m,m)，则CF = m - 3，AE = 6 - m，
∴m - 3 = 6 - m，解得m = 4.5，
∴点D的坐标为(4.5,4.5)；
②如图2，当点D在直线y = - x上时，过点D作DG⊥y轴，过点A作AH⊥GD交GD延长线于点H，
同理可得△CGD≌△DHA，
∴GC = DH，
设点D(m, - m)，则GC = 3 + m，DH = 6 - m，
∴3 + m = 6 - m，解得m = 1.5，
∴点D的坐标为(1.5, - 1.5)。


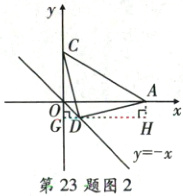
综上，点D的坐标为(4.5,4.5)或(1.5, - 1.5)。