《2025年初中毕业升学真题详解八年级数学上册北师大版陕西专版》

8. 如图,在$ Rt\triangle ABC$中,$\angle C=90°$,$D$为$AC$上一点。若$DA=DB=8$,$\triangle ABD$的面积为24,则$CD$的长是(D)。

A.3
B.4
C.6
D.$2\sqrt{7}$

答案： 8.D　[点拨]本题考查三角形的面积，勾股定理。
[解析]
∵$\angle C=90°$，$DA=DB=8$，$\triangle ABD$的面积为24，
∴$S_{\triangle ABD}=\frac{1}{2}AD· BC=24$，即$\frac{1}{2}×8BC=24$，
∴$BC=6$。在$Rt\triangle BCD$中，由勾股定理得$CD=\sqrt{DB^2-BC^2}=\sqrt{8^2-6^2}=2\sqrt{7}$。故选D。

9. 已知$\sqrt{x-3}+\sqrt{6-2x}+y=5$,则$\sqrt{5xy}$的值为(A)。

A.$5\sqrt{3}$
B.$5\sqrt{2}$
C.5
D.6

答案： 9.A　[点拨]本题考查二次根式有意义的条件，二次根式的化简求值。
[解析]由题意，得$\begin{cases}x-3\geq0\\6-2x\geq0\end{cases}$解得$x=3$，
∴$y=5$，
∴$\sqrt{5xy}=\sqrt{5×3×5}=5\sqrt{3}$。故选A。

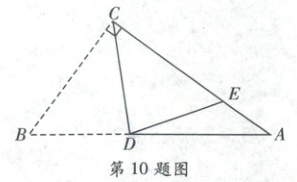
10. 右侧扫码·视频讲解 如图,在$ Rt\triangle ABC$中,$\angle ACB=90°$,$D$是$AB$上一点,将$\triangle BDC$沿$CD$折叠,点$B$的对应点$E$恰好落在$AC$边上。已知$BC=6$,$AE=2$,则$DE$的长为(C)。

A.$\frac{18}{7}$
B.$\frac{24}{7}$
C.$\frac{30}{7}$
D.$\frac{32}{7}$

答案：
10.C　[点拨]本题考查角平分线的性质，勾股定理，折叠的性质，三角形的面积。
[解析]如图，过点D作$DM\perp BC$于点M，作$DN\perp AC$于点N。由折叠可知，$\angle BCD=\angle ECD=\frac{1}{2}\angle ACB=45°$，$BC=CE=6$，$BD=DE$，
∴$AC=CE+AE=6+2=8$，$MD=DN$。在$Rt\triangle ABC$中，由勾股定理得$AB=\sqrt{AC^2+BC^2}=\sqrt{8^2+6^2}=10$。设$BD=DE=x$，点C到AB的距离为h，则$AD=AB-BD=10-x$，
∴$S_{\triangle BCD}=\frac{1}{2}BC· DM=\frac{1}{2}BD· h$，$S_{\triangle ACD}=\frac{1}{2}AC· DN=\frac{1}{2}AD· h$，
∴$6DM=xh$，$8DN=(10-x)h$，即$DM=\frac{xh}{6}$，$DN=\frac{(10-x)h}{8}$，
∴$\frac{xh}{6}=\frac{(10-x)h}{8}$，解得$x=\frac{30}{7}$，
∴$DE=\frac{30}{7}$。 故选C。

11. 16的算术平方根是4。

答案： 11.4　[点拨]本题考查算术平方根的定义。
[解析]
∵$4^2=16$，
∴16的算术平方根为4。故答案为4。

12. 比较大小:$\sqrt{13}-2$ ＜ $\frac{1}{3}$(填“＞”“＜”或“=”)

答案： 12.$＜$　[点拨]本题考查无理数的估算，实数大小比较。
[解析]
∵$3＜\sqrt{13}＜4$，
∴$1＜\sqrt{13}-2＜2$，
∴$\frac{1}{6}＜\frac{\sqrt{13}-2}{6}＜\frac{1}{3}$。故答案为$＜$。

13. 已知$\sqrt[3]{2.025}\approx1.265,\sqrt[3]{20.25}\approx2.726,$则$\sqrt[3]{2025}\approx$12.65。

答案： 13.12.65　[点拨]本题考查求一个数的立方根，理解立方根的定义是正确解答的前提。
[解析]
∵$\sqrt[3]{2.025}\approx1.265$，
∴$\sqrt[3]{2025}=\sqrt[3]{2.025×1000}=\sqrt[3]{2.025}×\sqrt[3]{1000}\approx1.265×10=12.65$。故答案为12.65。

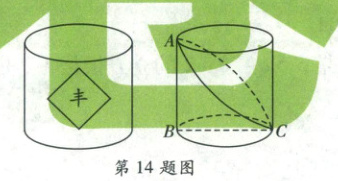
14. 右侧扫码·视频讲解 小彬用3D打印机制作了一个底面周长为30 cm,高为20 cm的圆柱粮仓模型,如图,$BC$是底面圆直径,$AB$是高,现要在此模型的侧面贴一圈彩色装饰带,使装饰带经过$A,C$两点(接头不计),则装饰带的长度最短为50cm。

答案：
14.50cm　[点拨]本题考查勾股定理的应用，熟练运用勾股定理是解题的关键。
[解析]如图，圆柱的侧面展开图为长方形，$AC=A'C$，且C为$BB'$的中点，$AB\perp BB'$。根据题意，可知$AB=20$cm，$BC=\frac{1}{2}×30=15$(cm)，
∴$AC=\sqrt{AB^2+BC^2}=\sqrt{20^2+15^2}=25$(cm)，
∴装饰带的长度最短为$2AC=2×25=50$(cm)。 故答案为50cm。

15. 已知实数a,b在数轴上的对应点如图所示,则$\sqrt{(a+2)^2}-\sqrt{(b-3)^2}+\sqrt{(a+b)^2}=$-1。

答案： 15.$-1$　[点拨]本题考查实数与数轴，二次根式的化简。
[解析]由数轴可得，$-2＜a＜0＜b＜2$，$|a|＞|b|$，
∴$a+2＞0$，$b-3＜0$，$a+b＜0$，
∴$\sqrt{(a+2)^2}-\sqrt{(b-3)^2}+\sqrt{(a+b)^2}=a+2-[-(b-3)]+[-(a+b)]=a+2+b-3-a-b=-1$。故答案为$-1$。

16. 右侧扫码·视频讲解 如图,在$\triangle ABC$中,$AB=24$,$AC=13$,$D$是线段$BC$上一点,连接$AD$,$AD=20$,$CD=21$,则$BD$的长为$12\sqrt{3}-16$。

答案：
16.$12\sqrt{3}-16$　[点拨]本题考查勾股定理和完全平方公式。
[解析]如图，过点A作$AE\perp BC$于点E，则$\angle AEB=\angle AEC=90°$。设$DE=n$，则$EC=21-n$。在$Rt\triangle AED$中，$AE^2=AD^2-DE^2=20^2-n^2$，在$Rt\triangle AEC$中，$AE^2=AC^2-EC^2=13^2-(21-n)^2$，
∴$20^2-n^2=13^2-(21-n)^2$，解得$n=16$，
∴$DE=16$，$EC=5$，$AE=12$。在$Rt\triangle AEB$中，$AE^2+BE^2=AB^2$，即$12^2+BE^2=24^2$，
∴$BE=12\sqrt{3}$，
∴$BD=BE-DE=12\sqrt{3}-16$。 故答案为$12\sqrt{3}-16$。

17. (12分)计算。
(1)$\sqrt{8}+\sqrt{32}-\sqrt{50}$;
(2)$\frac{\sqrt{27}+\sqrt{12}}{\sqrt{3}}-(\pi-3.14)^0$;
(3)$3\sqrt{8}×\frac{\sqrt{3}}{12}÷\sqrt{24}$;
(4)$\left(\sqrt{18}-\sqrt{\frac{1}{2}}\right)×\sqrt{8}$;
(5)$(\sqrt{2}+\sqrt{6})^2-(\sqrt{5}-2)(\sqrt{5}+2)$;
(6)$-1^{2024}+\sqrt{(-6)^2}+\sqrt[3]{27}+\vert1-\sqrt{3}\vert$。

答案： 17.[点拨]本题考查二次根式的混合运算，熟练掌握运算法则是解题的关键。
[解析]
(1)$\sqrt{8}+\sqrt{32}-\sqrt{50}=2\sqrt{2}+4\sqrt{2}-5\sqrt{2}=\sqrt{2}$。
(2)$\frac{\sqrt{27}+\sqrt{12}}{\sqrt{3}}-(\pi-3.14)^0=\sqrt{\frac{27}{3}}+\sqrt{\frac{12}{3}}-1=\sqrt{9}+\sqrt{4}-1=3+2-1=4$。
(3)$3\sqrt{8}×\frac{\sqrt{3}}{12}÷\sqrt{24}=\frac{3}{12}\sqrt{8×3×\frac{1}{24}}=\frac{\sqrt{24}}{4}×\frac{1}{\sqrt{24}}=\frac{1}{4}$。
(4)$(\sqrt{18}-\sqrt{\frac{1}{2}})×\sqrt{8}=\sqrt{18×8}-\sqrt{\frac{1}{2}×8}=\sqrt{144}-\sqrt{4}=12-2=10$。
(5)$(\sqrt{2}+\sqrt{6})^2-(\sqrt{5}-2)(\sqrt{5}+2)=(\sqrt{2})^2+2×\sqrt{2}×\sqrt{6}+(\sqrt{6})^2-[(\sqrt{5})^2-2^2]=2+4\sqrt{3}+6-(5-4)=7+4\sqrt{3}$。
(6)$-1^{2024}+\sqrt{(-6)^2}+\sqrt[3]{27}+|1-\sqrt{3}|=-1+6+3+\sqrt{3}-1=7+\sqrt{3}$。