2025年初中毕业升学真题详解八年级数学上册北师大版陕西专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年初中毕业升学真题详解八年级数学上册北师大版陕西专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第42页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
9. 如图,在一个长$AB$为$8\ \mathrm{cm}$,宽$AD$为$6\ \mathrm{cm}$的长方形木板上,放着一根长方体木块,木块较长的棱和木板的宽$AD$平行且棱长大于$AD$,木块从正面看是边长为$2\ \mathrm{cm}$的正方形,一只蚂蚁从点$A$出发到达$BC$边中点$M$需要走的最短路程为(

A.$10$
B.$3\sqrt{17}$
C.$\sqrt{205}$
D.$6\sqrt{5}$
B
)$\mathrm{cm}$。(从木板的上表面走)
A.$10$
B.$3\sqrt{17}$
C.$\sqrt{205}$
D.$6\sqrt{5}$
答案:
9.B [点拨]本题考查勾股定理与最短路径问题,解答本题的关键要明确两点之间线段最短。
[解析]如图所示,将木块展开;由题意得,展开后的长方形的长为$8 + 2 + 2 = 12( cm)$,宽为$6 cm$,即$BM = 3 cm$,$\therefore$一只蚂蚁从点$A$出发到达点$M$处需要走的最短路程为$\sqrt{12^{2}+3^{2}}=3\sqrt{17}( cm)$。
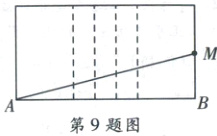
故选B。
9.B [点拨]本题考查勾股定理与最短路径问题,解答本题的关键要明确两点之间线段最短。
[解析]如图所示,将木块展开;由题意得,展开后的长方形的长为$8 + 2 + 2 = 12( cm)$,宽为$6 cm$,即$BM = 3 cm$,$\therefore$一只蚂蚁从点$A$出发到达点$M$处需要走的最短路程为$\sqrt{12^{2}+3^{2}}=3\sqrt{17}( cm)$。

故选B。
10. 直线$y = k_1x + 2$与$y = k_2x + b$相交于点$(2, 0)$,且两直线与$y$轴围成的三角形面积为$6$,$P(1, m)$是三角形内部(包括边上)的一点,则$m$的最大值与最小值之差为(
A.$3$
B.$\dfrac{3}{2}$
C.$3$或$\dfrac{3}{2}$
D.$3$或$6$
A
)。A.$3$
B.$\dfrac{3}{2}$
C.$3$或$\dfrac{3}{2}$
D.$3$或$6$
答案:
10.A [点拨]本题考查一次函数的图象,两条直线相交的问题,根据已知条件确定两个一次函数解析式是解题的关键。
[解析]$\because$直线$y = k_{1}x + 2$与$y = k_{2}x + b$相交于点$(2,0)$,$\therefore0 = 2k_{1}+2$,$0 = 2k_{2}+b$,解得$k_{1}=-1$,$k_{2}=-\frac{b}{2}$,$\therefore$两直线为$y=-x + 2$与$y=-\frac{b}{2}x + b$,设两直线$y=-x + 2$与$y=-\frac{b}{2}x + b$与$y$轴分别交于点$A,B$,则$A(0,2)$,$B(0,b)$,$AB = |b - 2|$,$\because$两直线与$y$轴围成的三角形面积为$6$,$\therefore\frac{1}{2}|b - 2|×2 = 6$,解得$b = 8$或$b = - 4$。当$b = 8$时,两直线为$y=-x + 2$与$y=-4x + 8$,如图1所示,$P(1,m)$是三角形内部(包括边上)的一点,
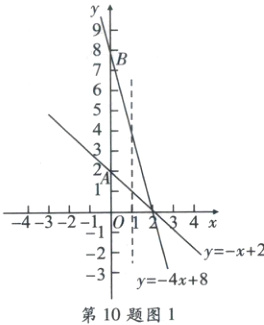
由图1可知,当$x = 1$时,$m$的最大值为$-4×1 + 8 = 4$,$m$的最小值为$-1 + 2 = 1$,$\therefore m$的最大值与最小值之差为$4 - 1 = 3$;当$b = - 4$时,两直线为$y=-x + 2$与$y=2x - 4$,如图2,
$P(1,m)$是三角形内部(包括边上)的一点,由图2可知,当$x = 1$时,$m$的最大值为$-1 + 2 = 1$,$m$的最小值为$2×1 - 4 = - 2$,
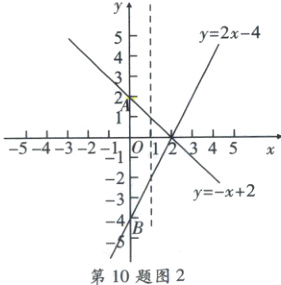
$\therefore m$的最大值与最小值之差为$1-(-2)=3$。综上所述,$m$的最大值与最小值之差为$3$。故选A。
10.A [点拨]本题考查一次函数的图象,两条直线相交的问题,根据已知条件确定两个一次函数解析式是解题的关键。
[解析]$\because$直线$y = k_{1}x + 2$与$y = k_{2}x + b$相交于点$(2,0)$,$\therefore0 = 2k_{1}+2$,$0 = 2k_{2}+b$,解得$k_{1}=-1$,$k_{2}=-\frac{b}{2}$,$\therefore$两直线为$y=-x + 2$与$y=-\frac{b}{2}x + b$,设两直线$y=-x + 2$与$y=-\frac{b}{2}x + b$与$y$轴分别交于点$A,B$,则$A(0,2)$,$B(0,b)$,$AB = |b - 2|$,$\because$两直线与$y$轴围成的三角形面积为$6$,$\therefore\frac{1}{2}|b - 2|×2 = 6$,解得$b = 8$或$b = - 4$。当$b = 8$时,两直线为$y=-x + 2$与$y=-4x + 8$,如图1所示,$P(1,m)$是三角形内部(包括边上)的一点,

由图1可知,当$x = 1$时,$m$的最大值为$-4×1 + 8 = 4$,$m$的最小值为$-1 + 2 = 1$,$\therefore m$的最大值与最小值之差为$4 - 1 = 3$;当$b = - 4$时,两直线为$y=-x + 2$与$y=2x - 4$,如图2,
$P(1,m)$是三角形内部(包括边上)的一点,由图2可知,当$x = 1$时,$m$的最大值为$-1 + 2 = 1$,$m$的最小值为$2×1 - 4 = - 2$,

$\therefore m$的最大值与最小值之差为$1-(-2)=3$。综上所述,$m$的最大值与最小值之差为$3$。故选A。
11. 如图,实数$\sqrt{6}$在数轴上的对应点可能是

C
点。
答案:
11.C [点拨]本题考查算术平方根,数轴表示数,掌握算术平方根的定义是解决本题的关键。
[解析]$\because\sqrt{4}<\sqrt{6}<\sqrt{9}$,$\therefore2<\sqrt{6}<3$,$\therefore$数轴上点$C$所表示的数可能是$\sqrt{6}$。故答案为C。
[解析]$\because\sqrt{4}<\sqrt{6}<\sqrt{9}$,$\therefore2<\sqrt{6}<3$,$\therefore$数轴上点$C$所表示的数可能是$\sqrt{6}$。故答案为C。
12. 平面直角坐标系中,点$A$在第二象限,若点$A$到$x$轴的距离为$3$,到$y$轴的距离为$4$,则点$A$的坐标为
(-4,3)
。
答案:
12.$(-4,3)$ [点拨]本题考查点的坐标,熟练掌握平面直角坐标系内点的坐标特征是解题的关键,第二象限,点的横坐标为负数,纵坐标为正数,再根据点$A$到$x$轴的距离为$3$,到$y$轴的距离为$4$,即可确定点$A$坐标。
[解析]$\because$点$A$在第二象限,$\therefore$点$A$横坐标为负数,纵坐标为正数,$\because A$到$x$轴的距离为$3$,到$y$轴的距离为$4$,$\therefore$点$A$的坐标为$(-4,3)$。故答案为$(-4,3)$。
[解析]$\because$点$A$在第二象限,$\therefore$点$A$横坐标为负数,纵坐标为正数,$\because A$到$x$轴的距离为$3$,到$y$轴的距离为$4$,$\therefore$点$A$的坐标为$(-4,3)$。故答案为$(-4,3)$。
13. 已知正比例函数$y = (m - 1)x^{|m|}$的图象经过第一、三象限,则$m$的值为
2
。
答案:
13.2 [点拨]本题考查正比例函数的性质,熟知正比例函数的图象与性质是解题的关键。
[解析]由题知,因为函数$y=(m - 1)x^{5 - m^{2}}$是正比例函数,所以$5 - m^{2}=1$,解得$m=\pm2$。又因为此正比例函数的图象经过第一、三象限,所以$m - 1>0$,解得$m>1$,所以$m$的值为$2$。故答案为$2$。
[解析]由题知,因为函数$y=(m - 1)x^{5 - m^{2}}$是正比例函数,所以$5 - m^{2}=1$,解得$m=\pm2$。又因为此正比例函数的图象经过第一、三象限,所以$m - 1>0$,解得$m>1$,所以$m$的值为$2$。故答案为$2$。
14. 若点$A(-1, y_1)$和点$B(2, y_2)$在一次函数$y = -3x + b$的图象上,则$y_1$
>
$y_2$。(填“$>$”“$<$”或“$=$”)
答案:
14.$>$ [点拨]本题考查一次函数的性质,牢记“$k>0$,$y$随$x$的增大而增大;$k<0$,$y$随$x$的增大而减小”是解题的关键。
[解析]$\because k=-3<0$,$\therefore y$随$x$的增大而减小,又$\because$点$A(-1,y_{1})$和点$B(2,y_{2})$在一次函数$y=-3x + b$的图象上,且$-1<2$,$\therefore y_{1}>y_{2}$。故答案为$>$。
[解析]$\because k=-3<0$,$\therefore y$随$x$的增大而减小,又$\because$点$A(-1,y_{1})$和点$B(2,y_{2})$在一次函数$y=-3x + b$的图象上,且$-1<2$,$\therefore y_{1}>y_{2}$。故答案为$>$。
15. 已知$\triangle ABC$中,$AB = 15$,$AC = 6\sqrt{5}$,且$BC$边上的高$AD = 12$,则$BC$的长为
15或3
。
答案:
15.$15$或$3$ [点拨]本题考查勾股定理,熟练掌握勾股定理是解题的关键。
[解析]如图1,$\because$在$\triangle ABC$中,$AB = 15$,$AC = 6\sqrt{5}$,$BC$边上的高$AD = 12$,$\therefore BD=\sqrt{AB^{2}-AD^{2}}=\sqrt{15^{2}-12^{2}}=9$,$CD=\sqrt{AC^{2}-AD^{2}}=\sqrt{(6\sqrt{5})^{2}-12^{2}}=6$,$\therefore BC=BD + DC = 15$。
如图2,$\because$在$ Rt\triangle ABD$中,$AB = 15$,$AD = 12$,$BD=\sqrt{AB^{2}-AD^{2}}=\sqrt{15^{2}-12^{2}}=9$,$CD=\sqrt{AC^{2}-AD^{2}}=\sqrt{(6\sqrt{5})^{2}-12^{2}}=6$,$\therefore BC=BD - CD = 9 - 6 = 3$。
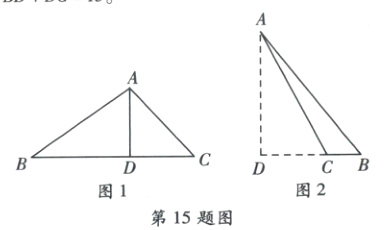
综上所述,$BC$的长为$15$或$3$。故答案为$15$或$3$。
15.$15$或$3$ [点拨]本题考查勾股定理,熟练掌握勾股定理是解题的关键。
[解析]如图1,$\because$在$\triangle ABC$中,$AB = 15$,$AC = 6\sqrt{5}$,$BC$边上的高$AD = 12$,$\therefore BD=\sqrt{AB^{2}-AD^{2}}=\sqrt{15^{2}-12^{2}}=9$,$CD=\sqrt{AC^{2}-AD^{2}}=\sqrt{(6\sqrt{5})^{2}-12^{2}}=6$,$\therefore BC=BD + DC = 15$。
如图2,$\because$在$ Rt\triangle ABD$中,$AB = 15$,$AD = 12$,$BD=\sqrt{AB^{2}-AD^{2}}=\sqrt{15^{2}-12^{2}}=9$,$CD=\sqrt{AC^{2}-AD^{2}}=\sqrt{(6\sqrt{5})^{2}-12^{2}}=6$,$\therefore BC=BD - CD = 9 - 6 = 3$。

综上所述,$BC$的长为$15$或$3$。故答案为$15$或$3$。
16. 如图,$C$是直线$y = 3x + 6$在第二象限上的一个点,点$C$关于$x$轴对称的点为$D$,关于$y$轴对称的点为$E$,连接$DE, CE$,则线段$DE$的最小值为
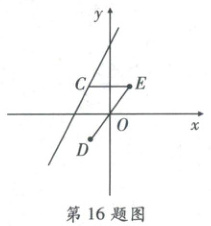
$\frac{6\sqrt{10}}{5}$
。
答案:
16.$\frac{6\sqrt{10}}{5}$ [点拨]本题考查一次函数的图象和性质,矩形的性质和判定,轴对称的性质,三角形中位线定理,两点之间线段最短,勾股定理等知识。正确作出辅助线是解题的关键。
[解析]如图,设$DC$交$x$轴于点$P$,$CE$交$y$轴于点$Q$,直线交$x$轴于点$A$,交$y$轴于点$B$,$DE$交$y$轴于点$M$,连接$OC$。
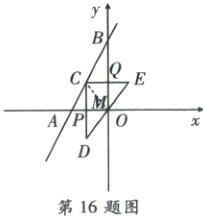
$\because$直线$y = 3x + 6$,$\therefore$当$x = 0$时,$y = 6$;当$y = 0$时,$x = - 2$,$\therefore B(0,6)$,$A(-2,0)$,$\therefore AB=\sqrt{OA^{2}+OB^{2}}=2\sqrt{10}$,根据对称可得,$PC = PD$,$CQ = EQ$,$CD// y$轴,$CE// x$轴,$\therefore QM=\frac{1}{2}CD$,$DM = EM$。$\because CQ// PO$,$PC// OQ$,$\therefore$四边形$CPOQ$是平行四边形。$\because\angle POQ = 90^{\circ}$,$\therefore$平行四边形$CPOQ$是矩形,$\therefore PC = OQ$,$\therefore QM = OQ$,$\therefore$点$M$与点$O$重合,$\therefore DE$过原点$O$。$\because\angle DCE = 90^{\circ}$,$\therefore DE = 2OC$,$\therefore$当$OC$最小时,$DE$最小,当$OC\perp AB$时,$OC$最小。$\because S_{\triangle AOB}=\frac{1}{2}AB· OC=\frac{1}{2}OA· OB$,$\therefore OC=\frac{OA· OB}{AB}=\frac{2×6}{2\sqrt{10}}=\frac{3\sqrt{10}}{5}$,$\therefore DE$的最小值为$\frac{6\sqrt{10}}{5}$。
故答案为$\frac{6\sqrt{10}}{5}$。
16.$\frac{6\sqrt{10}}{5}$ [点拨]本题考查一次函数的图象和性质,矩形的性质和判定,轴对称的性质,三角形中位线定理,两点之间线段最短,勾股定理等知识。正确作出辅助线是解题的关键。
[解析]如图,设$DC$交$x$轴于点$P$,$CE$交$y$轴于点$Q$,直线交$x$轴于点$A$,交$y$轴于点$B$,$DE$交$y$轴于点$M$,连接$OC$。

$\because$直线$y = 3x + 6$,$\therefore$当$x = 0$时,$y = 6$;当$y = 0$时,$x = - 2$,$\therefore B(0,6)$,$A(-2,0)$,$\therefore AB=\sqrt{OA^{2}+OB^{2}}=2\sqrt{10}$,根据对称可得,$PC = PD$,$CQ = EQ$,$CD// y$轴,$CE// x$轴,$\therefore QM=\frac{1}{2}CD$,$DM = EM$。$\because CQ// PO$,$PC// OQ$,$\therefore$四边形$CPOQ$是平行四边形。$\because\angle POQ = 90^{\circ}$,$\therefore$平行四边形$CPOQ$是矩形,$\therefore PC = OQ$,$\therefore QM = OQ$,$\therefore$点$M$与点$O$重合,$\therefore DE$过原点$O$。$\because\angle DCE = 90^{\circ}$,$\therefore DE = 2OC$,$\therefore$当$OC$最小时,$DE$最小,当$OC\perp AB$时,$OC$最小。$\because S_{\triangle AOB}=\frac{1}{2}AB· OC=\frac{1}{2}OA· OB$,$\therefore OC=\frac{OA· OB}{AB}=\frac{2×6}{2\sqrt{10}}=\frac{3\sqrt{10}}{5}$,$\therefore DE$的最小值为$\frac{6\sqrt{10}}{5}$。
故答案为$\frac{6\sqrt{10}}{5}$。
17. (10 分)计算。
(1) $\sqrt{24} ÷ \sqrt{2} - \sqrt{8} × \sqrt{6} + \sqrt{\dfrac{1}{3}}$;
(2) $(\sqrt{5} + 2)(\sqrt{5} - 2) + (2\sqrt{3} - 1)^2$。
(1) $\sqrt{24} ÷ \sqrt{2} - \sqrt{8} × \sqrt{6} + \sqrt{\dfrac{1}{3}}$;
(2) $(\sqrt{5} + 2)(\sqrt{5} - 2) + (2\sqrt{3} - 1)^2$。
答案:
17.[点拨]本题考查二次根式的混合运算,平方差公式,完全平方公式等知识,解题的关键是掌握二次根式的混合运算法则。
[解析]
(1)$\sqrt{24}÷\sqrt{2}-\sqrt{8}×\sqrt{6}+\sqrt{\frac{1}{3}}$
$=\sqrt{24÷2}-\sqrt{8×6}+\frac{\sqrt{3}}{3}$
$=2\sqrt{3}-4\sqrt{3}+\frac{\sqrt{3}}{3}$
$=-\frac{5\sqrt{3}}{3}$。
(2)$(\sqrt{5}+2)(\sqrt{5}-2)+(2\sqrt{3}-1)^{2}$
$=5 - 4 + 12 - 4\sqrt{3}+1$
$=14 - 4\sqrt{3}$。
[解析]
(1)$\sqrt{24}÷\sqrt{2}-\sqrt{8}×\sqrt{6}+\sqrt{\frac{1}{3}}$
$=\sqrt{24÷2}-\sqrt{8×6}+\frac{\sqrt{3}}{3}$
$=2\sqrt{3}-4\sqrt{3}+\frac{\sqrt{3}}{3}$
$=-\frac{5\sqrt{3}}{3}$。
(2)$(\sqrt{5}+2)(\sqrt{5}-2)+(2\sqrt{3}-1)^{2}$
$=5 - 4 + 12 - 4\sqrt{3}+1$
$=14 - 4\sqrt{3}$。
18. (5 分)如图,在平面直角坐标系中。
(1) 图中点$B$的坐标是
(2) 点$B$关于$y$轴对称的点$D$的坐标是
(3) 已知点$A$的坐标是$(-3, 0)$,若点$B$关于原点对称的点是$C$,请在方格纸中画出$\triangle ABC$,$\triangle ABC$的面积是

(1) 图中点$B$的坐标是
(-4,5)
;(2) 点$B$关于$y$轴对称的点$D$的坐标是
(4,5)
;(3) 已知点$A$的坐标是$(-3, 0)$,若点$B$关于原点对称的点是$C$,请在方格纸中画出$\triangle ABC$,$\triangle ABC$的面积是
15
。
答案:
18.[点拨]本题考查作图——旋转变换、轴对称,熟练掌握中心对称的性质、轴对称的性质是解答本题的关键。
[解析]
(1)由题图可得,点$B$的坐标是$(-4,5)$。故答案为$(-4,5)$。
(2)点$B$关于$y$轴对称的点$D$的坐标是$(4,5)$。故答案为$(4,5)$。
(3)如图,$\triangle ABC$即为所求。
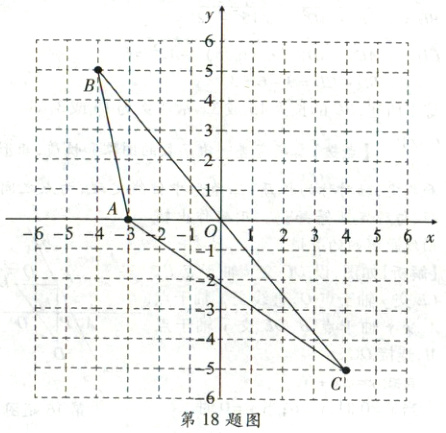
$\triangle ABC$的面积$=S_{\triangle AOB}+S_{\triangle AOC}=\frac{1}{2}×3×5+\frac{1}{2}×3×5=15$。
故答案为$15$。
18.[点拨]本题考查作图——旋转变换、轴对称,熟练掌握中心对称的性质、轴对称的性质是解答本题的关键。
[解析]
(1)由题图可得,点$B$的坐标是$(-4,5)$。故答案为$(-4,5)$。
(2)点$B$关于$y$轴对称的点$D$的坐标是$(4,5)$。故答案为$(4,5)$。
(3)如图,$\triangle ABC$即为所求。

$\triangle ABC$的面积$=S_{\triangle AOB}+S_{\triangle AOC}=\frac{1}{2}×3×5+\frac{1}{2}×3×5=15$。
故答案为$15$。
查看更多完整答案,请扫码查看


