2025年初中毕业升学真题详解八年级数学上册北师大版陕西专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年初中毕业升学真题详解八年级数学上册北师大版陕西专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第36页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
18. (6分)已知一个正数的两个平方根分别是$5a - 1$和$a - 5$,且$2b - 4$的立方根为$-2$。
(1) 求$a$,$b$的值;
(2) 求$5a - 2b$的算术平方根。
(1) 求$a$,$b$的值;
(2) 求$5a - 2b$的算术平方根。
答案:
18.[点拨]本题考查平方根,算术平方根,立方根,熟练掌握这几个定义是解题的关键。
[解析]
(1)根据题意得,$5a - 1 + a - 5 = 0$,解得$a = 1$。$\because 2b - 4$的立方根为$-2$,$\therefore 2b - 4 = - 8$,解得$b = - 2$。
(2)由
(1)得,$a = 1$,$b = - 2$,$\therefore 5a - 2b = 5×1 - 2×(-2)=5-(-4)=5 + 4 = 9$。$\because 9$的算术平方根是$3$,$\therefore 5a - 2b$的算术平方根是$3$。
[解析]
(1)根据题意得,$5a - 1 + a - 5 = 0$,解得$a = 1$。$\because 2b - 4$的立方根为$-2$,$\therefore 2b - 4 = - 8$,解得$b = - 2$。
(2)由
(1)得,$a = 1$,$b = - 2$,$\therefore 5a - 2b = 5×1 - 2×(-2)=5-(-4)=5 + 4 = 9$。$\because 9$的算术平方根是$3$,$\therefore 5a - 2b$的算术平方根是$3$。
19. (6分)$\triangle ABC$在平面直角坐标系中的位置如图所示,$A$,$B$,$C$三点都在格点上。
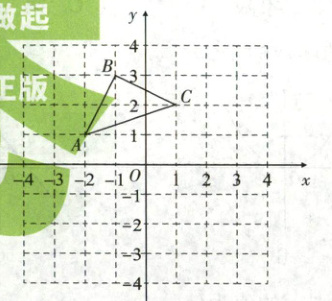
(1) $\triangle ABC$关于$x$轴对称的图形为$\triangle A_1B_1C_1$(其中$A$与$A_1$,$B$与$B_1$,$C$与$C_1$相对应),在图中画出$\triangle A_1B_1C_1$;
(2) $P$是$x$轴上一点,则$AP + CP$的最小值是

(1) $\triangle ABC$关于$x$轴对称的图形为$\triangle A_1B_1C_1$(其中$A$与$A_1$,$B$与$B_1$,$C$与$C_1$相对应),在图中画出$\triangle A_1B_1C_1$;
(2) $P$是$x$轴上一点,则$AP + CP$的最小值是
$3\sqrt{2}$
。
答案:
19.[点拨]本题考查作图——轴对称变换、轴对称——最短路线问题、勾股定理,熟练掌握轴对称的性质、勾股定理是解答本题的关键。
[解析]
(1)如图,$\triangle A_{1}B_{1}C_{1}$即为所求。
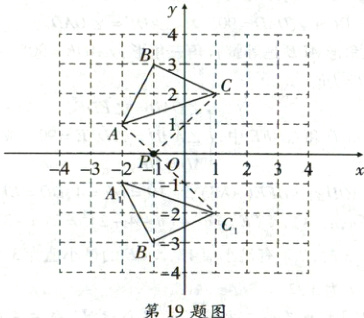
(2)如图,连接$AC_{1}$交$x$轴于点$P$,连接$CP$,此时$AP + CP = AP + C_{1}P = AC_{1}$为最小值,由勾股定理得$AC_{1}=\sqrt{3^{2}+3^{2}} = 3\sqrt{2}$。$\therefore AP + CP$的最小值是$3\sqrt{2}$。故答案为$3\sqrt{2}$。
19.[点拨]本题考查作图——轴对称变换、轴对称——最短路线问题、勾股定理,熟练掌握轴对称的性质、勾股定理是解答本题的关键。
[解析]
(1)如图,$\triangle A_{1}B_{1}C_{1}$即为所求。

(2)如图,连接$AC_{1}$交$x$轴于点$P$,连接$CP$,此时$AP + CP = AP + C_{1}P = AC_{1}$为最小值,由勾股定理得$AC_{1}=\sqrt{3^{2}+3^{2}} = 3\sqrt{2}$。$\therefore AP + CP$的最小值是$3\sqrt{2}$。故答案为$3\sqrt{2}$。
20. (8分) 近日,陕西通信技术在西北地区率先迈入“双万兆”时代,双万兆,指的是“$5G - A$无线+$F5G - A$有线”光网技术能力均超万兆。$5G - A$是基于第五代移动通信技术的演进和增强版具备通感一体、无源物联、内生智能等“超能力”,能够满足更为复杂和多样化的应用场景需求。过去的20年里,通信行业经历了从$2G$,$3G$,$4G$到$5G$的飞速发展,某电信公司也适时推出流量卡,包含了甲、乙两种方案供用户选择:甲种方案每月收取月租费$25$元,流量费为$0.5$元/$GB$;乙种方案不收取月租费,流量费为$1.8$元/$GB$。假设每月使用流量为$x\ GB$,甲种方案的每月费用为$y_1$元,乙种方案的每月费用为$y_2$元。(注:$GB$是一种流量的计算单位)
(1) 分别写出$y_1$,$y_2$与$x$的关系式;
(2) 若小王平均每月使用$22GB$的流量,通过计算说明他选择哪种方案更划算?
(1) 分别写出$y_1$,$y_2$与$x$的关系式;
(2) 若小王平均每月使用$22GB$的流量,通过计算说明他选择哪种方案更划算?
答案:
20.[点拨]本题考查一次函数的应用,解答本题的关键是明确题意,求出相应的函数解析式。
[解析]
(1)由题意可得,$y_{1}=0.5x + 25$,$y_{2}=1.8x$。
(2)当$x = 22$时,$y_{1}=0.5×22 + 25 = 36$,$y_{2}=1.8×22 = 39.6$,$\because 36<39.6$,$\therefore$小王选择甲种方案更划算。
[解析]
(1)由题意可得,$y_{1}=0.5x + 25$,$y_{2}=1.8x$。
(2)当$x = 22$时,$y_{1}=0.5×22 + 25 = 36$,$y_{2}=1.8×22 = 39.6$,$\because 36<39.6$,$\therefore$小王选择甲种方案更划算。
查看更多完整答案,请扫码查看


