《2025年初中毕业升学真题详解八年级数学上册北师大版陕西专版》

9. 右侧扫码·视频讲解 如图，四边形$ ABCD $中，$ AD // BC $，$ \angle A = 90° $，$ AB = BC = 2AD = 4 $，边$ CD $的垂直平分线分别交$ AB $，$ CD $于点$ E $，$ F $，则$ AE $的长为(B)。

A.$ \sqrt{13} $
B.$ \frac{7}{2} $
C.7
D.$ \frac{21}{4} $

答案：
9. B【点拨】本题考查线段垂直平分线的性质、勾股定理的应用。
【解析】如图，连接ED，EC，
∵EF是边CD的垂直平分线，
∴ED = EC，在Rt△ADE中，DE² = AD² + AE²，在Rt△BCE中，CE² = BE² + BC²，
∴AD² + AE² = BE² + BC²，
即2² + AE² = (4 - AE)² + 4²，解得AE = $\frac{7}{2}$。故选B。

10. 右侧扫码·视频讲解 如图，在$ \triangle ABC $中，$ AB = AC $，$ E $是边$ AB $上一点，连接$ CE $，在$ BC $的左侧作$ BF // AC $，且$ BF = AE $，连接$ CF $。若$ AC = 26 $，$ BC = 20 $，则四边形$ EBFC $的面积为(B)。

A.120
B.240
C.360
D.480

答案：
10. B【点拨】本题考查勾股定理的应用，等腰三角形的性质，正确作出辅助线是解题的关键。
【解析】
∵AB = AC，
∴∠ABC = ∠ACB。
∵BF//AC，
∴∠ACB = ∠CBF，
∴∠ABC = ∠CBF，
∴BC平分∠ABF。如图，过点C作CM⊥AB，CN⊥BF，垂足分别为M，N，
∴CM = CN，
∵$S_{\triangle ACE}=\frac{1}{2}AE· CM$，$S_{\triangle CBF}=\frac{1}{2}BF· CN$，BF = AE，
∴$S_{\triangle CBF}=S_{\triangle ACE}$，
∴四边形EBFC的面积 = $S_{\triangle CBF}+S_{\triangle CBE}=S_{\triangle ACE}+S_{\triangle CBE}=S_{\triangle CBA}$，
∵AC = 26，
∴AB = 26，设AM = x，则BM = 26 - x，由勾股定理，得CM² = AC² - AM² = BC² - BM²，
∴26² - x² = 20² - (26 - x)²，
解得x = $\frac{238}{13}$，
∴CM = $\sqrt{26^{2}-(\frac{238}{13})^{2}}=\frac{240}{13}$，
∴$S_{\triangle ABC}=\frac{1}{2}AB· CM=\frac{1}{2}×26×\frac{240}{13}$ = 240。
∴四边形EBFC的面积为240。故选B。

11. 在平面直角坐标系中，点$ P(7, -4) $关于原点对称的点的坐标是 (-7,4) 。

答案： 11. (-7,4)【点拨】本题考查关于原点对称的点的坐标。
【解析】
∵关于原点对称的点的横坐标互为相反数，纵坐标互为相反数，
∴点P(7,-4)关于原点对称的点的坐标是(-7,4)。故答案为(-7,4)。

12. 将一次函数$ y = -3x + 6 $的图象向左平移$ m $个单位长度后得到一个正比例函数的图象，则$ m $的值为 2 。

答案： 12. 2【点拨】本题考查一次函数图象的平移，正比例函数的定义。
【解析】将一次函数y = -3x + 6的图象向左平移m个单位长度后，得到y = -3(x + m) + 6的图象，把(0,0)代入，得0 = -3m + 6，解得m = 2。故答案为2。

13. 甲、乙、丙、丁四名同学参加立定跳远训练，他们成绩的平均数相同，方差如下：$ s_甲^2 = 2.5 $，$ s_乙^2 = 3.1 $，$ s_丙^2 = 7 $，$ s_丁^2 = 0.9 $，则这四名同学中成绩最稳定的是 丁 。

答案： 13. 丁【点拨】本题考查方差的意义。
【解析】
∵$s_{甲}^{2}=2.5$，$s_{乙}^{2}=3.1$，$s_{丙}^{2}=7$，$s_{丁}^{2}=0.9$，
∴丁的方差最小，
∴成绩最稳定的是丁。故答案为丁。

14. 如图，小正方形组成的$ 3 × 2 $网格中，每个小正方形的顶点称为格点。点$ A $，$ B $，$ C $，$ D $，$ M $，$ N $均在格点上，其中$ A $，$ B $，$ C $，$ D $四个点中能与点$ M $，$ N $构成一个直角三角形的是点 C 。

答案： 14. C【点拨】本题考查勾股定理的逆定理。
【解析】
∵AM² = 1² = 1，MN² = 1² + 2² = 5，AN² = 1² + 1² = 2，
∴AM² + AN² ≠ MN²，
∴△AMN不是直角三角形，故A点不符合题意；
∵MN² = 1² + 2² = 5，NB² = 1² + 2² = 5，BM² = 2² = 4，
∴MN² + MB² ≠ BN²，
∴△BMN不是直角三角形，故B点不符合题意；
∵MN² = 1² + 2² = 5，CM² = 1² + 3² = 10，CN² = 2² + 2² = 5，
∴MN² + CN² = MC²，
∴△CMN是直角三角形，故C点符合题意；
∵MN² = 1² + 2² = 5，ND² = 2² + 2² = 8，DM² = 3² = 9，
∴MN² + DN² ≠ MD²，
∴△DMN不是直角三角形，故D点不符合题意。故答案为C。

15. 如图，在$ \triangle ABC $中，$ \angle ABC = 45° $，$ AD \perp BC $，$ BE $平分$ \angle ABC $，分别交$ AC $，$ AD $于点$ E $，$ F $。若$ DF = \sqrt{2} $，$ AC = 4 + 2\sqrt{2} $，则$ \angle AEB $的度数为 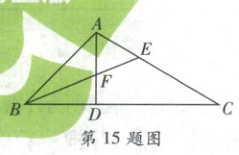52.5° 。

答案： 15. 52.5°【点拨】本题考查角平分线的定义、等腰直角三角形的性质、勾股定理、含30°角的直角三角形的性质。
【解析】如题图，过点F作FH⊥AB，垂足为H，
∵BE平分∠ABC，AD⊥BC，
∴HF = DF = $\sqrt{2}$。
∵∠ABC = 45°，
∴∠BAD = 45°，
∴△AFH是等腰直角三角形，
∴AH = HF = $\sqrt{2}$。在Rt△AHF中，AF = $\sqrt{AH^{2}+HF^{2}} = 2$，
∴AD = 2 + $\sqrt{2}$，
∵AC = 4 + 2$\sqrt{2}$，
∴∠C = 30°，
∴∠AEB = ∠C + ∠EBC = ∠C + $\frac{1}{2}$∠ABC = 30° + 22.5° = 52.5°。故答案为52.5°。

16. 右侧扫码·视频讲解 已知方程组$ \begin{cases}3x + 2y = 15 \\ 2x + 3y = 3k - 1\end{cases}$的解满足$ x + y = 4 $，则$ k = $ ______ 。

答案： 16. 2【点拨】本题考查解二元一次方程组。
【解析】
∵方程组$\begin{cases}3x + 2y = 15\\2x + 3y = 3k - 1\end{cases}$的解满足x + y = 4，
∴方程组$\begin{cases}3x + 2y = 15\\x + y = 4\end{cases}$的解满足2x + 3y = 3k - 1，
解方程组$\begin{cases}3x + 2y = 15\\x + y = 4\end{cases}$得$\begin{cases}x = 7\\y = -3\end{cases}$，
把$\begin{cases}x = 7\\y = -3\end{cases}$代入方程2x + 3y = 3k - 1中，得k = 2。故答案为2。

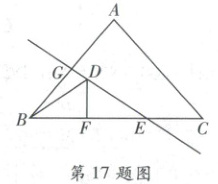
17. 右侧扫码·视频讲解 如图，等腰$ \triangle ABC $的面积为 189，底边$ BC = 18 $，点$ F $在边$ BC $上，且$ CF = 2BF $，$ EG $是腰$ AB $的垂直平分线，若点$ D $在$ EG $上运动，则$ \triangle BDF $周长的最小值为 15$\sqrt{2}$ + 6 。

答案：
17. 15$\sqrt{2}$ + 6【点拨】本题考查轴对称——最短路径问题，涉及线段垂直平分线的性质、三角形面积公式及勾股定理的应用。
【解析】如图，过点A作AH⊥BC于点H，连接AF，AD，
∵等腰△ABC的面积为189，底边BC = 18，
∴$\frac{1}{2}$AH·BC = 189，BH = $\frac{1}{2}$BC = 9，
∴AH = 21。
∵EG是腰AB的垂直平分线，
∴BD = AD，
∴△BDF的周长为BD + DF + BF = AD + DF + BF ≥ AF + BF，则AF + BF的值为△BDF周长的最小值，
∵CF = 2BF，
∴BF = $\frac{1}{3}$BC = 6，
∴HF = BH - BF = 3，
在Rt△AFH中，AF = $\sqrt{AH^{2}+HF^{2}} = 15\sqrt{2}$，
∴AF + BF = 15$\sqrt{2}$ + 6，
∴△BDF周长的最小值为15$\sqrt{2}$ + 6。故答案为15$\sqrt{2}$ + 6。

18. （10 分）解方程组。
(1) $ \begin{cases} 2x - y = 3 \\ 3(x + 2) + 2(y - 4) = 6 \end{cases} $；
(2) $ \begin{cases} \frac{x}{2} - \frac{y + 1}{3} = 1 \\ 3x + 2y = 10 \end{cases} $。

答案： 18.【点拨】本题考查解二元一次方程组。
【解析】
(1)$\begin{cases}2x - y = 3\\3(x + 2) + 2(y - 4) = 6\end{cases}$
整理得$\begin{cases}2x - y = 3,①\\3x + 2y = 8,②\end{cases}$
①×2 + ②，得7x = 14，解得x = 2，
把x = 2代入①，得4 - y = 3，解得y = 1，
所以方程组的解为$\begin{cases}x = 2\\y = 1\end{cases}$
(2)$\begin{cases}\frac{x}{2}-\frac{y + 1}{3}=1\\3x + 2y = 10\end{cases}$
①×6，得3x - 2y = 8，③
②+③，得6x = 18，解得x = 3，
把x = 3代入②，得9 + 2y = 10，解得y = $\frac{1}{2}$，
所以方程组的解为$\begin{cases}x = 3\\y = \frac{1}{2}\end{cases}$