《2025年初中毕业升学真题详解八年级数学上册北师大版陕西专版》

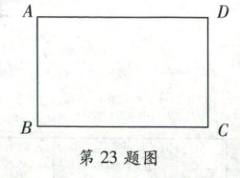
23. （10 分）如图，有一张长、宽比为$3:2$的长方形纸片$ABCD$，面积为$96\ \mathrm{cm}^2$。
(1) 分别求长方形纸片的长和宽；
(2) 小丽想沿这张长方形纸片边的方向裁剪一块长、宽比为$6:5$的新长方形，使其面积为$90\ \mathrm{cm}^2$，请问她能裁出符合要求的长方形吗？试说明理由。

答案： 23.[点拨]本题考查算术平方根，实数比较大小，准确熟练地进行计算是解题的关键。
[解析]
(1)设长方形纸片的长为$3x cm$，宽为$2x cm$，由题意得$3x·2x = 96$，解得$x = 4$或$x = - 4$（舍去），$\therefore$长方形的长为$12 cm$，宽为$8 cm$。
(2)她不能裁出符合要求的长方形，理由如下：设新长方形纸片的长为$6a cm$，宽为$5a cm$，由题意得$6a·5a = 90$，解得$a=\sqrt{3}$或$a = -\sqrt{3}$（舍去），$\therefore$新长方形的长为$6\sqrt{3} cm$，宽为$5\sqrt{3} cm$。$\because(6\sqrt{3})^{2}=108$，$12^{2}=144$，$(5\sqrt{3})^{2}=75$，$8^{2}=64$，$\because75＞64$，$\therefore5\sqrt{3}＞8$，$\therefore$她不能裁出符合要求的长方形。

24. （10 分）用充电器给某手机充电时，其屏幕画面显示目前电量为$40\%$。经测试，在用快速充电器和普通充电器对该手机充电时，其电量$y$（单位：$\%$）与充电时间$x$（单位：分钟）的函数图象分别为图中的线段$AC, AB$。
根据以上信息，回答下列问题。
(1) 求线段$AB$对应的函数表达式；
(2) 先用普通充电器充电$a$分钟，电量达到$70\%$后，感觉充电较慢，再改为快速充电器充电，电量充满时充电总时长为$b$分钟。通过计算求出$a, b$所对应的值，并在图中画出改用快充充电器后电量$y$与充电时间$x$的函数图象$DE$。

答案：
24.[点拨]本题考查一次函数的应用，掌握待定系数法求函数表达式是解题的关键。
[解析]
(1)设线段$AB$对应的函数表达式为$y = kx + b(k,b$为常数，且$k\neq0)$，把坐标$A(0,40)$和$B(60,100)$分别代入$y = kx + b$，得$\begin{cases}b = 40\\60k + b = 100\end{cases}$，解得$\begin{cases}k = 1\\b = 40\end{cases}$。
$\therefore$线段$AB$对应的函数表达式为$y = x + 40(0\leqslant x\leqslant60)$。
(2)当$y = 70$时，得$x + 40 = 70$，解得$x = 30$，$\therefore a = 30$。设线段$AC$对应的函数表达式为$y = k_{1}x + b_{1}(k_{1},b_{1}$为常数，且$k_{1}\neq0)$，把坐标$A(0,40)$和$C(20,100)$分别代入$y = k_{1}x + b_{1}$，得$\begin{cases}b_{1} = 40\\20k_{1}+b_{1}=100\end{cases}$，解得$\begin{cases}k_{1}=3\\b_{1}=40\end{cases}$。
$\therefore$线段$AC$对应的函数表达式为$y = 3x + 40(0\leqslant x\leqslant20)$。当$y = 70$时，得$3x + 40 = 70$，解得$x = 10$；当$y = 100$时，得$3x + 40 = 100$，解得$x = 20$，$\therefore$改用快充充电器后的充电时间为$20 - 10 = 10( 分钟)$，$\therefore b = 30 + 10 = 40$。$\because$当$x = 30$时，$y = 70$；当$x = 40$时，$y = 100$，$\therefore$函数图象$DE$如图所示。

25. （12 分）
【思维启迪】
(1) 如图 1，$AD$是$\triangle ABC$的中线，延长$AD$到点$E$，使$DE = AD$，连接$BE$，则$AC$与$BE$的数量关系为BE = AC，位置关系为AC//BE；
【思维应用】
(2) 如图 2，在$\triangle ABC$中，$\angle ACB = 90°$，$D$为$\triangle ABC$内一点，连接$AD, DC$，延长$DC$到点$E$，使$CE = CD$，连接$BE$，若$AD \perp BE$，请用等式表示$AB, AD, BE$之间的数量关系，并说明理由；
【思维探索】
(3) 如图 3，在$\triangle ABC$中，$\angle ACB = 90°$，$AC = BC$，$D$为$AB$的中点，点$E$在射线$DB$上（点$E$不与点$B$、点$D$重合），连接$CE$，过点$B$作$BF \perp CE$，垂足为$F$，连接$FD$。若$CB = \sqrt{29}$，$BF = 2$，请直接写出$FD$的长。

答案：
25.[点拨]本题是三角形综合题和倍长中线问题，考查全等三角形的判定和性质，勾股定理，平行线的性质和判定等知识，掌握全等三角形的判定定理和性质定理是解题的关键，并运用类比的方法解决问题。
[解析]
(1)如图1，

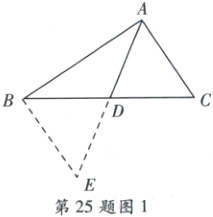
$\because D$是$BC$的中点，$\therefore BD = CD$。$\because\angle ADC=\angle EDB$，$AD = DE$，$\therefore\triangle ADC\cong\triangle EDB(SAS)$，$\therefore BE = AC$，$\angle C=\angle DBE$，$\therefore AC// BE$。故答案为$BE = AC$，$AC// BE$。
(2)$AD^{2}+BE^{2}=AB^{2}$。理由如下：如图2，延长$BC$至点$F$，使得$CF = BC$，连接$DF$，$AF$，

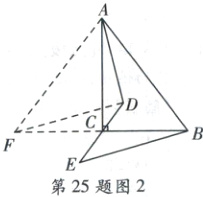
$\because\angle ACB = 90^{\circ}$，即$AC\perp BF$，$\therefore AC$是$BF$的垂直平分线，$\therefore AF = AB$。$\because CE = DC$，$\angle FCD=\angle BCE$，$\therefore\triangle FCD\cong\triangle BCE(SAS)$，$\therefore BE = FD$，$\angle CBE=\angle CFD$，$\therefore DF// BE$。$\because AD\perp BE$，$\therefore AD\perp FD$。在$ Rt\triangle ADF$中，由勾股定理得$AD^{2}+DF^{2}=AF^{2}$，$\therefore AD^{2}+BE^{2}=AB^{2}$。
(3)因为点$E$在射线$DB$上，所以分两种情况：
①当点$E$在线段$DB$上时，延长$FD$至点$H$，使得$DH = DF$，连接$AH$并延长交直线$FC$的延长线于点$G$，如图3，

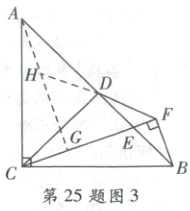
$\because D$是$AB$的中点，$\therefore DA = DB$。又$\because DH = DF$，$\angle ADH=\angle BDF$，$\triangle ADH\cong\triangle BDF(SAS)$，$\therefore\angle DAH=\angle DBF$，$\therefore AH// BF$。$\because BF\perp CE$，$\therefore AG\perp CE$。$\because\angle ACB = 90^{\circ}$，$\therefore\angle CAG+\angle ACG=\angle ACG+\angle BCF = 90^{\circ}$，$\therefore\angle CAG=\angle BCF$。$\because\angle AGC=\angle CFB = 90^{\circ}$，$CA = CB$，$\therefore\triangle CAG\cong\triangle BCF(AAS)$，$\therefore AG = CF$，$CG = BF = AH = 2$，$\therefore HG = FG$。在$ Rt\triangle BFC$中，由勾股定理得，$CF=\sqrt{BC^{2}-BF^{2}}=\sqrt{(\sqrt{29})^{2}-2^{2}}=5$，$\therefore HG = FG = 5 - 2 = 3$，在$ Rt\triangle HGF$中，由勾股定理得，$HF=\sqrt{HG^{2}+GF^{2}}=\sqrt{3^{2}+3^{2}}=3\sqrt{2}$，$DF=\frac{1}{2}HF=\frac{3\sqrt{2}}{2}$；
②当点$E$在$DB$的延长线上时，延长$FD$至点$H$，使得$DH = DF$，连接$HA$并延长交直线$FC$的延长线于点$G$，如图4，

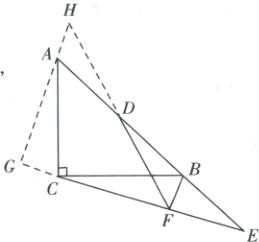
$\because D$是$AB$的中点，$\therefore DA = DB$。又$\because DH = DF$，$\angle ADH=\angle BDF$，$\triangle ADH\cong\triangle BDF(SAS)$，$\therefore\angle DAH=\angle DBF$，$AH// BF$。$\because BF\perp CE$，$\therefore AG\perp CE$。$\because\angle ACB = 90^{\circ}$，$\therefore\angle CAG+\angle ACG=\angle ACG+\angle BCF = 90^{\circ}$，$\therefore\angle CAG=\angle BCF$。$\because\angle G=\angle CFB = 90^{\circ}$，$CA = CB$，$\therefore\triangle CAG\cong\triangle BCF(AAS)$，$\therefore AG = CF$，$CG = BF = AH = 2$，$\therefore HG = FG$。在$ Rt\triangle BFC$中，由勾股定理求得$CF = 5$，$\therefore HG = FG = 2 + 5 = 7$，在$ Rt\triangle HGF$中，由勾股定理得，$HF=\sqrt{HG^{2}+GF^{2}}=\sqrt{7^{2}+7^{2}}=7\sqrt{2}$，$\therefore DF=\frac{1}{2}HF=\frac{7\sqrt{2}}{2}$。
综上所述，$FD$的长为$\frac{3\sqrt{2}}{2}$或$\frac{7\sqrt{2}}{2}$。