《2025年初中毕业升学真题详解八年级数学上册北师大版陕西专版》

19. （5 分）函数$y = (k - 1)x + k + 2$是关于$x$的正比例函数。
(1) 求$k$的值；
(2) 当$y = -3$时，求$x$的值。

答案： 19.[点拨]本题考查正比例函数的定义及正比例函数的性质，解题的关键是了解正比例函数的一般形式。
[解析]
(1)$\because$该函数是正比例函数，$\therefore k + 2 = 0$，解得$k = - 2$。
(2)当$k = - 2$时，该函数的解析式为$y = - 3x$，当$y = - 3$时，$-3x = - 3$，解得$x = 1$。

20. （6 分）如图，在$\triangle ABC$中，$BC = 6$，$AC = 8$，$DE \perp AB$，$DE = 7$，$\triangle ABE$的面积为$35$。求$\triangle ACB$的面积。

答案： 20.[点拨]本题考查三角形的面积，勾股定理的逆定理的应用，解此题的关键是求出$\triangle ABC$是直角三角形。
[解析]$\because DE = 7$，$\triangle ABE$的面积为$35$，$\therefore\frac{1}{2}· AB·7 = 35$，$\therefore AB = 10$。$\because BC = 6$，$AC = 8$，$\therefore AC^{2}+BC^{2}=AB^{2}$，$\therefore\angle C = 90^{\circ}$，$\therefore S_{\triangle ABC}=\frac{1}{2}×6×8 = 24$。

21. （6 分）若$x, y$为实数，且满足$\sqrt{2x - 1} + |y^3 + 1| = 0$，求$\dfrac{1}{20}(x^2 + y^2)$的平方根。

答案： 21.[点拨]本题考查非负数的性质、算术平方根、绝对值、平方根，正确求出$x,y$的值是解题的关键。
[解析]$\because\sqrt{2x - 1}+|y^{3}+1| = 0$，又$\because\sqrt{2x - 1}\geqslant0$，$|y^{3}+1|\geqslant0$，$\therefore2x - 1 = 0$，$y^{3}+1 = 0$，$\therefore x=\frac{1}{2}$，$y = - 1$，$\therefore\frac{1}{20}(x^{2}+y^{2})=\frac{1}{20}×(\frac{1}{4}+1)=\frac{1}{16}$。$\because\frac{1}{16}$的平方根是$\pm\frac{1}{4}$，$\therefore\frac{1}{20}(x^{2}+y^{2})$的平方根是$\pm\frac{1}{4}$。

22. （8 分）某校开展红色主题研学活动，开启红色文化之旅，在延安一博物馆门口离地面一定高度的墙上$D$处，装有一个由传感器控制的迎宾门铃，人只要移动到距离该门口$2.4\ \mathrm{m}$时，门铃就会自动发出“延安欢迎您”的语音，如图，一个身高$1.6\ \mathrm{m}$的学生刚走到$B$处（学生头顶在$A$处），门铃恰好自动响起，此时测得门铃到地面的距离$DC$和门铃到该学生头顶的距离$DA$相等（$AB \perp BC, DC \perp BC$）。请你计算门铃到地面的距离$DC$为多少米？

答案：
22.[点拨]本题考查勾股定理的应用，熟练掌握勾股定理，正确作出辅助线构造直角三角形是解题的关键。
[解析]由题意知，$AD = CD$，$BC = 2.4 m$，$AB = 1.6 m$，$\angle ABC=\angle DCB = 90^{\circ}$，

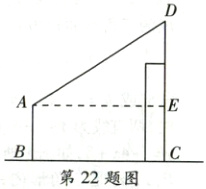
如图，过点$A$作$AE\perp CD$于点$E$，则$CE = AB = 1.6 m$，$AE = BC = 2.4 m$，设迎宾门铃距离地面$x m$，则$AD = CD = x m$，$DE=(x - 1.6) m$，在$ Rt\triangle AED$中，由勾股定理得$AE^{2}+DE^{2}=AD^{2}$，即$2.4^{2}+(x - 1.6)^{2}=x^{2}$，解得$x = 2.6$。
答：门铃距离地面$2.6 m$。