《2025年人教金学典同步解析与测评高中物理选择性必修第一册人教版》

例题 1 如图 4.1 - 4 所示，眼睛从水面上方观察正下方水中的 $ P $ 点，其深度与实际深度的关系如何？

答案： 设水中P点实际深度为$ h $（即$ PA = h $），视深为$ h' $（即$ P'A = h' $）。
由折射定律：$ n = \frac{\sin\theta_1}{\sin\theta_2} $。
因入射角$ \theta_2 $、折射角$ \theta_1 $很小，近似有$ \sin\theta_2 \approx \tan\theta_2 = \frac{AB}{h} $，$ \sin\theta_1 \approx \tan\theta_1 = \frac{AB}{h'} $。
代入折射定律：$ n = \frac{\frac{AB}{h'}}{\frac{AB}{h}} = \frac{h}{h'} $，解得$ h' = \frac{h}{n} $。
水的折射率$ n \approx \frac{4}{3} $，故$ h' \approx \frac{3}{4}h $。
结论：垂直观察时，视深为实际深度的$ \frac{1}{n} $，水中物体视深约为实际深度的$ \frac{3}{4} $。

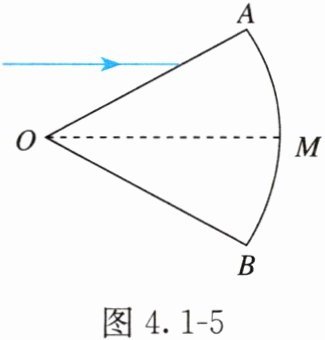
例题 2 如图 4.1 - 5 所示，扇形 $ AOB $（半径为 $ R $）为透明柱状介质的横截面，圆心角 $ \angle AOB = 60° $。一束平行于角平分线 $ OM $ 的单色光由 $ OA $ 射入介质，折射光线平行于 $ OB $ 且恰好射向 $ M $（不考虑反射光线，已知光在真空中的传播速度为 $ c $）。求：
(1) 从 $ AMB $ 面射出的出射光线与进入介质的入射光线的偏向角；
(2) 光在介质中的传播时间。

答案： （1）由几何关系，入射光线平行于OM，OM与OA夹角30°，则入射角θ₁=60°（入射光线与OA法线夹角）。折射光线平行于OB，折射角θ₂=30°（折射光线与OA法线夹角）。由折射定律：n=sinθ₁/sinθ₂=sin60°/sin30°=√3。
在AMB面，法线为OM，折射光线与OM夹角30°（入射角θ₂'=30°）。由折射定律：n=sinθ₁'/sinθ₂'，得sinθ₁'=n sinθ₂'=√3×1/2=√3/2，θ₁'=60°。
偏向角α=θ₁+θ₁'-(θ₂+θ₂')=60°+60°-(30°+30°)=60°。
（2）光在介质中传播距离d=R/2÷cos30°=R/2÷(√3/2)=R/√3=√3R/3。
介质中光速v=c/n=c/√3，传播时间t=d/v=(√3R/3)/(c/√3)=R/c。
（1）60°；（2）R/c。