《2025年人教金学典同步解析与测评高中物理选择性必修第一册人教版》

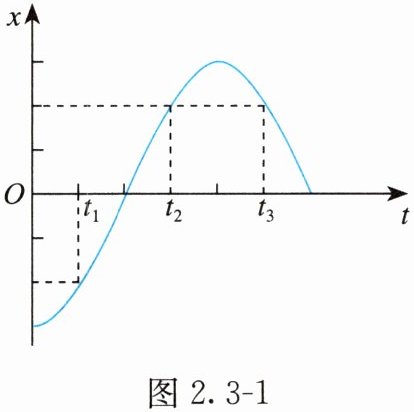
例题 1 图 2.3 - 1 是水平弹簧振子做简谐运动的振动图像。
(1) 请判断在 $ t _ { 1 } $ 时刻与 $ t _ { 2 } $ 时刻，小球的位移 $ x $、速度 $ v $、加速度 $ a $、弹性势能 $ E _ { \mathrm { p } } $、动能 $ E _ { \mathrm { k } } $、回复力 $ F $ 中有哪些物理量完全相同，并说明理由。
(2) 请判断在 $ t _ { 1 } $ 时刻与 $ t _ { 3 } $ 时刻，小球的位移 $ x $、速度 $ v $、加速度 $ a $、弹性势能 $ E _ { \mathrm { p } } $、动能 $ E _ { \mathrm { k } } $、回复力 $ F $ 中有哪些物理量完全相同，并说明理由。

答案：
(1) 完全相同的物理量：速度$v$、动能$E_{k}$、弹性势能$E_{p}$。
理由：
位移$x$：由图像知，$t_1$时刻位移为负，$t_2$时刻位移为正，大小相等、方向相反，故$x$不同；
回复力$F$：由$F=-kx$，位移方向相反，故$F$大小相等、方向相反，不同；
加速度$a$：由$a=-\frac{kx}{m}$，与位移方向相同（因负号），故$a$大小相等、方向相反，不同；
速度$v$：$x-t$图像切线斜率表示速度，两时刻斜率相同，故$v$大小相等、方向相同，相同；
动能$E_{k}$：由$E_{k}=\frac{1}{2}mv^2$，$v$相同，故$E_{k}$相同；
弹性势能$E_{p}$：由$E_{p}=\frac{1}{2}kx^2$，$x$大小相等，故$E_{p}$相同。
(2) 完全相同的物理量：弹性势能$E_{p}$、动能$E_{k}$。
理由：
位移$x$：两时刻位移大小相等、方向相反（或方向相同但速度方向相反），故$x$不同；
回复力$F$：由$F=-kx$，位移方向相反，故$F$大小相等、方向相反，不同；
加速度$a$：由$a=-\frac{kx}{m}$，与位移方向相同，故$a$大小相等、方向相反，不同；
速度$v$：$x-t$图像切线斜率方向相反（一正一负），故$v$大小相等、方向相反，不同；
动能$E_{k}$：由$E_{k}=\frac{1}{2}mv^2$，$v$大小相等，故$E_{k}$相同；
弹性势能$E_{p}$：由$E_{p}=\frac{1}{2}kx^2$，$x$大小相等，故$E_{p}$相同。

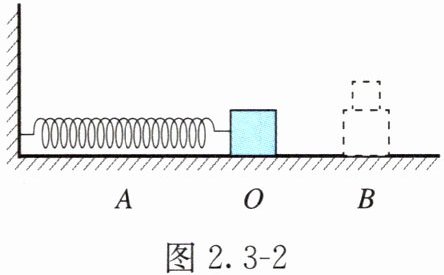
例题 2 如图 2.3 - 2 所示，一物块在光滑水平面上的 $ A $、$ B $ 两点间做简谐运动，平衡位置为 $ O $，已知物块的质量为 $ m _ { 0 } $。若物块运动到 $ B $ 点时将一质量为 $ m $ 的物体放到物块的上面，$ m $ 和 $ m _ { 0 } $ 无相对运动而一起运动，请分析物块（包含上面物体）的最大速度 $ v _ { \mathrm { m } } $、最大动能 $ E _ { \mathrm { km } } $、最大势能 $ E _ { \mathrm { pm } } $、最大振幅 $ A _ { \mathrm { m } } $、最大机械能 $ E _ { \mathrm { m } } $ 如何变化。

答案： 最大势能$E_{pm}$不变；最大机械能$E_{m}$不变；最大振幅$A_{m}$不变；最大动能$E_{km}$不变；最大速度$v_{m}$变小。

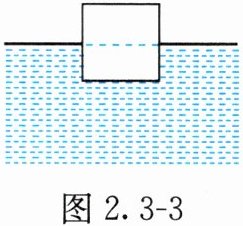
例题 3 一质量为 $ m $、横截面积为 $ S $ 的正方体木块，放在水面上静止（平衡），如图 2.3 - 3 所示。现用力向下将其压入水中某一深度后（未浸没）撤掉外力，木块在水面上下振动，试判断木块的振动是否为简谐运动。

答案： 要判断木块的振动是否为简谐运动，需分析其回复力是否满足 $ F=-kx $。
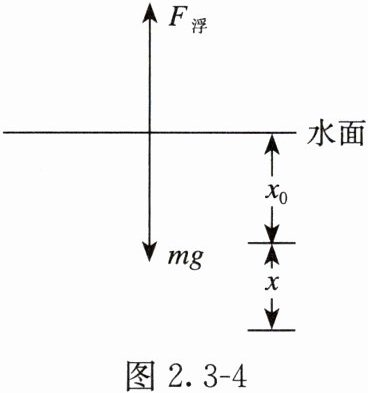
1. 确定平衡位置：木块静止时，重力与浮力平衡，合力为0，此位置为平衡位置。设此时浸入水中深度为$ x_0 $，有$ mg=\rho g S x_0 $。
2. 规定正方向：取向下为正方向。
3. 分析回复力：当木块偏离平衡位置向下位移为$ x $时，浸入深度为$ x_0 + x $，浮力$ F_{浮}=\rho g S(x_0 + x) $。回复力$ F=mg - F_{浮} $，代入$ mg=\rho g S x_0 $得：
$ F=\rho g S x_0 - \rho g S(x_0 + x)=-\rho g S x $。
4. 判断条件：回复力$ F=-kx $，其中$ k=\rho g S $为常数，满足简谐运动条件。
结论：木块的振动是简谐运动。