第76页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
2. 利用因式分解进行简便计算:$ 80×3.5^{2}+160×3.5×1.5 + 80×1.5^{2} $.
答案:
2000
3. 已知$ a^{2}+b^{2}-4a + 6b + 13 = 0 $,求$ a + b $的值.
答案:
由$a^2+b^2-4a+6b+13=0$,得$(a-2)^2+(b+3)^2=0$,$\therefore a=2$,$b=-3$,$\therefore a+b=-1$.
4. 数学活动.
数学中,常对同一个量(图形的面积、点的个数、三角形的内角和等)用两种不同的方法计算,从而建立相等关系,我们把这一思想称为“算两次”.“算两次”也被称作富比尼原理,是一种重要的数学思想. 例如:对于一个图形,通过不同的方法计算图形的面积可以得到一个数学等式.
计算如图1的面积,把图1看作一个大正方形,它的面积是$ (a + b)^{2} $;如果把图1看作是由2个长方形和2个小正方形组成的,它的面积为$ a^{2}+2ab + b^{2} $,由此得到$ (a + b)^{2}= a^{2}+2ab + b^{2} $.
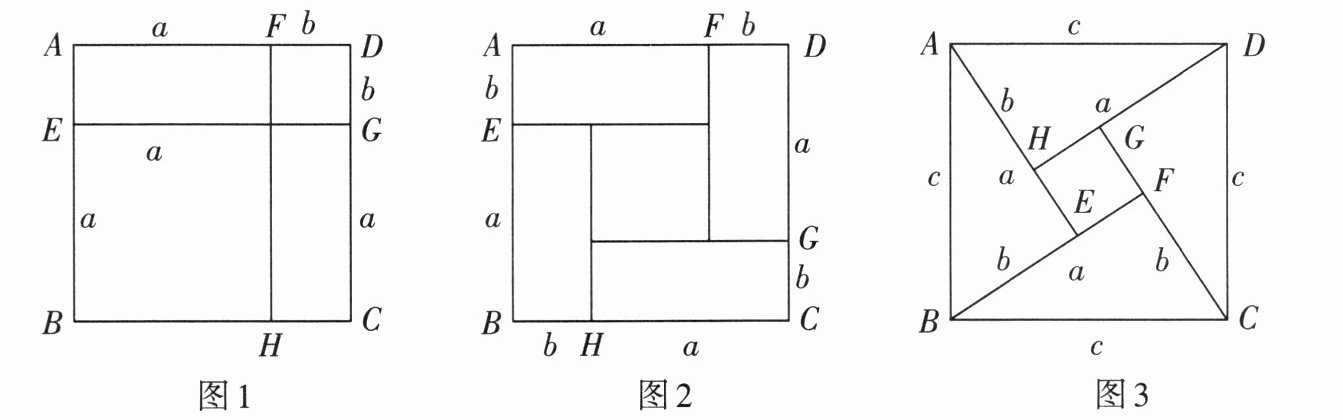
请利用上述数学思想解决下列问题:
(1)如图2,正方形$ ABCD 是由四个边长分别为 a,b $的长方形和中间一个小正方形组成的,用不同的方法对图2的面积进行计算,你发现的等式是______(用$ a,b $表示);
(2)如图3,四个三角形都是全等的直角三角形,用不同的代数式表示大正方形的面积,由此得到的等式为______(用$ a,b,c $表示);
(3)请进一步化简(2)题的等式,你发现直角三角形三边之间存在的关系了吗?如果直角三角形的两条直角边长分别为$ a,b $,斜边为$ c $,你发现的等式为______(用$ a,b,c $表示).
数学中,常对同一个量(图形的面积、点的个数、三角形的内角和等)用两种不同的方法计算,从而建立相等关系,我们把这一思想称为“算两次”.“算两次”也被称作富比尼原理,是一种重要的数学思想. 例如:对于一个图形,通过不同的方法计算图形的面积可以得到一个数学等式.
计算如图1的面积,把图1看作一个大正方形,它的面积是$ (a + b)^{2} $;如果把图1看作是由2个长方形和2个小正方形组成的,它的面积为$ a^{2}+2ab + b^{2} $,由此得到$ (a + b)^{2}= a^{2}+2ab + b^{2} $.

请利用上述数学思想解决下列问题:
(1)如图2,正方形$ ABCD 是由四个边长分别为 a,b $的长方形和中间一个小正方形组成的,用不同的方法对图2的面积进行计算,你发现的等式是______(用$ a,b $表示);
(2)如图3,四个三角形都是全等的直角三角形,用不同的代数式表示大正方形的面积,由此得到的等式为______(用$ a,b,c $表示);
(3)请进一步化简(2)题的等式,你发现直角三角形三边之间存在的关系了吗?如果直角三角形的两条直角边长分别为$ a,b $,斜边为$ c $,你发现的等式为______(用$ a,b,c $表示).
答案:
(1)$(a+b)^2=(a-b)^2+4ab$
(2)$c^2=2ab+(a-b)^2$
(3)$a^2+b^2=c^2$
(1)$(a+b)^2=(a-b)^2+4ab$
(2)$c^2=2ab+(a-b)^2$
(3)$a^2+b^2=c^2$
查看更多完整答案,请扫码查看


