《2025年新课程课堂同步练习册八年级数学上册人教版》

1. 计算$(a + b)(-a - b)$的结果是( )

A.$a^{2}-b^{2}$
B.$-a^{2}-b^{2}$
C.$a^{2}-2ab + b^{2}$
D.$-a^{2}-2ab - b^{2}$

答案： D

2. 如图1,边长为$(m + 3)的正方形纸片剪出一个边长为m$的正方形之后,余下部分又剪拼成一个长方形(不重叠无缝隙),若拼成的长方形一边长为$3$,则另一边长是( )


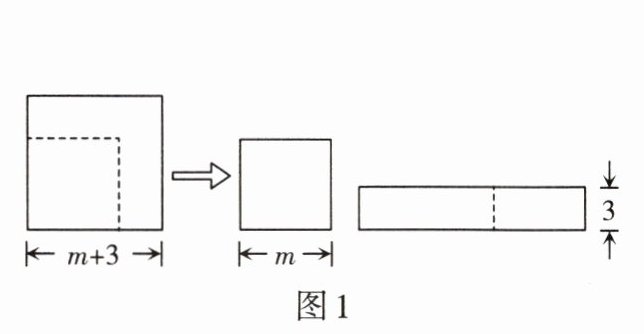
A.$2m + 3$
B.$2m + 6$
C.$m + 3$
D.$m + 6$

答案： A

3. 如图2,一块直径为$a + b$的圆形钢板,从中挖去直径分别为$a与b$的两个小圆. 则剩下的钢板(阴影部分)的面积为( )


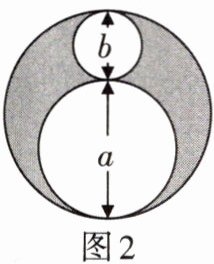
A.$\frac{\pi ab}{2}$
B.$\frac{\pi ab}{4}$
C.$2\pi ab$
D.$\pi ab$

答案： A

4. “杨辉三角”(如图3),也叫“贾宪三角”,是中国古代数学无比睿智的成就之一,被后世广泛运用. 用“杨辉三角”可以解释$(a + b)^{n}(n = 1,2,3,4)$的展开式(按$a$的次数由大到小的顺序)的系数规律. 例如,在“杨辉三角”中第$3行的3个数1,2,1$,恰好对应着$(a + b)^{2}的展开式a^{2}+2ab + b^{2}$中各项的系数；第$4行的4个数1,3,3,1$,恰好对应着$(a + b)^{3}的展开式a^{3}+3a^{2}b + 3ab^{2}+b^{3}$中各项的系数；等等. 当$n是大于4$的自然数时,上述规律仍然成立. 则$(a + b)^{7}的展开式中含a^{4}$的系数( )


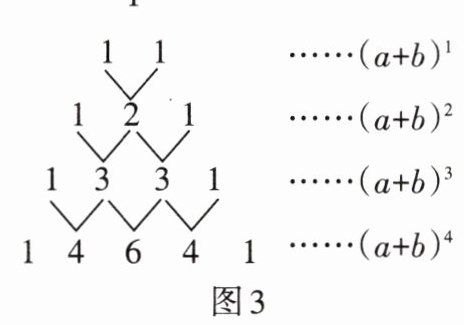
A.$21$

B.$1$
C.$35$
D.$7$

答案： C

1. (1)$a + b - c = a + ($______$)$；(2)$a - b + c - d = (a - d)-($______$)$；(3)$a - b + c = ($______$) + c$；(4)$-a - b + c = -($______$) + c$；(5)$a - b + c = a-($______$)$；(6)$a + b + c = a-($______$)$.

答案：
(1)$b - c$
(2)$b - c$
(3)$a - b$
(4)$a + b$
(5)$b - c$
(6)$-b - c$

2. $x^{2}+y^{2}= (x + y)^{2}-$______$=(x - y)^{2}+$______.

答案： $2xy$,$2xy$

3. $(x + y)^{2}= (x - y)^{2}+$______；$(x - y)^{2}= (x + y)^{2}-$______.

答案： $4xy$,$4xy$

1. 运用乘法公式计算：
(1)$(a + 2b - 3c)(a - 2b + 3c)$
(2)$(2x - y - 1)(2x + y - 1)$
(3)$(a - b - c)^{2}$
(4)$(x + 2y - 1)^{2}$

答案：
(1)$a^2 - 4b^2 - 9c^2 + 12bc$
(2)$4x^2 - 4x + 1 - y^2$
(3)$a^2 + b^2 + c^2 - 2ab - 2ac + 2bc$
(4)$x^2 + 4y^2 + 1 + 4xy - 2x - 4y$