《2025年新课程课堂同步练习册八年级数学上册人教版》

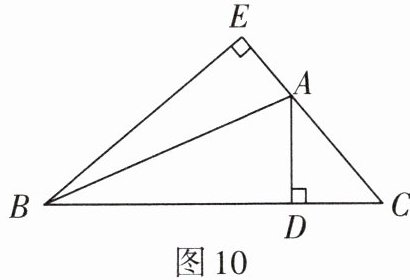
2. 如图 10,$ AD $,$ BE $ 分别是 $ \triangle ABC $ 的高,$ AC = 5 $,$ BC = 12 $,$ BE = 9 $,求 $ AD $ 的长.

答案：
∵AD,BE分别是△ABC的高,
∴S△ABC=1/2BC·AD=1/2AC·BE,
∴BC·AD=AC·BE.
∵AC=5,BC=12,BE=9,
∴12AD=5×9,
∴AD=15/4.

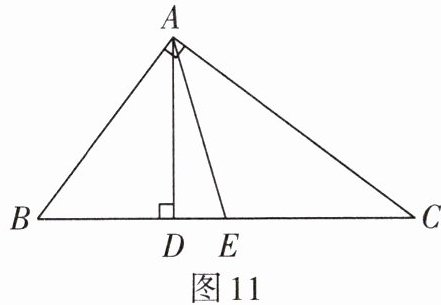
3. 如图 11,已知 $ AD $,$ AE $ 分别是 $ \triangle ABC $ 的边 $ BC $ 上的高和中线,$ AB = 12 cm $,$ AC = 16 cm $,$ BC = 20 cm $,$ \angle BAC = 90° $.
(1)求 $ AD $ 的长；
(2)求 $ \triangle ABE $ 的面积；
(3)求 $ \triangle ACE $ 和 $ \triangle ABE $ 的周长之差.

答案：
(1)
∵∠BAC=90°,AD是边BC上的高,
∴S△ABC=1/2AB·AC=1/2BC·AD,
∴AD=AB·AC/BC=12×16/20=9.6(cm),即AD=9.6 cm.
(2)
∵AE是边BC的中线,BC=20 cm,
∴BE=EC=1/2BC=1/2×20=10(cm). 由
(1)可知AD=9.6 cm,
∴S△ABE=1/2BE·AD=1/2×10×9.6=48(cm²),
∴△ABE的面积是48 cm².
(3)
∵AE为BC边上的中线,
∴BE=CE,
∴△ACE的周长-△ABE的周长=AC+AE+CE-(AB+BE+AE)=AC-AB=16-12=4(cm),即△ACE和△ABE的周长的差是4 cm.

4. 综合与实践：在学习完三角形的“与三角形有关的线段”后,某数学兴趣小组进行了有关内容的探究学习.

答案：

∵△ABC的中线AD=6,BE=3,
∴S△ABD=S△ACD,F是△ABC的重心,
∴AF=2/3AD=4,BF=2/3BE=2,
∴DF=6-4=2. 如图所示,作AH⊥BE于点H,则S△ABF=1/2BF·AH.
∵AH≤AF,
∴当AH=AF=4时,S△ABF取得最大值为1/2×2×4=4,
∴S△BDF的最大值为1/2×2×2=2,
∴S△ABD的最大值为2+4=6,S△ABC的最大值为2×6=12.