第46页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
2. 如图9,$AC$,$DB相交于点O$,$AB = DC$,$\angle A= \angle D$.
求证:(1)$\triangle ABO\cong\triangle DCO$;(2)$\angle OBC= \angle OCB$.
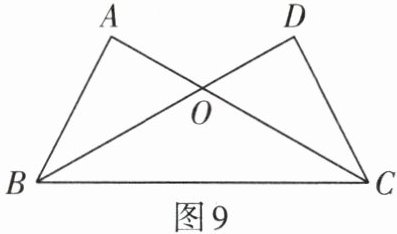
求证:(1)$\triangle ABO\cong\triangle DCO$;(2)$\angle OBC= \angle OCB$.

答案:
(1)证明:在$\triangle ABO$与$\triangle DCO$中,$\left\{\begin{array}{l} \angle A=\angle D,\\ \angle AOB=\angle DOC,\\ AB=DC,\end{array}\right.\therefore \triangle ABO\cong \triangle DCO(AAS)$.
(2)证明:$\because \triangle ABO\cong \triangle DCO,\therefore OB=OC,\therefore \angle OBC=\angle OCB$.
(1)证明:在$\triangle ABO$与$\triangle DCO$中,$\left\{\begin{array}{l} \angle A=\angle D,\\ \angle AOB=\angle DOC,\\ AB=DC,\end{array}\right.\therefore \triangle ABO\cong \triangle DCO(AAS)$.
(2)证明:$\because \triangle ABO\cong \triangle DCO,\therefore OB=OC,\therefore \angle OBC=\angle OCB$.
3. 如图10,在$\triangle ABC$中,$AB = AC$,$AD\perp BC于点D$,$CE\perp AB于点E$,$AE = CE$.
求证:(1)$\triangle AEF\cong\triangle CEB$;(2)$AF = 2CD$.
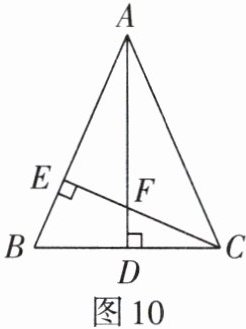
求证:(1)$\triangle AEF\cong\triangle CEB$;(2)$AF = 2CD$.

答案:
证明:
(1)$\because AD\perp BC,CE\perp AB,\therefore \angle B+\angle BAD=90^{\circ},\angle B+\angle BCE=90^{\circ},\therefore \angle EAF=\angle ECB$. 在$\triangle AEF$和$\triangle CEB$中,$\left\{\begin{array}{l} \angle AEF=\angle CEB=90^{\circ},\\ AE=CE,\\ \angle EAF=\angle ECB,\end{array}\right.\therefore \triangle AEF\cong \triangle CEB(ASA)$.
(2)$\because \triangle AEF\cong \triangle CEB,\therefore AF=BC$. $\because AB=AC,AD\perp BC,\therefore BD=CD,\therefore AF=BC=2CD$.
(1)$\because AD\perp BC,CE\perp AB,\therefore \angle B+\angle BAD=90^{\circ},\angle B+\angle BCE=90^{\circ},\therefore \angle EAF=\angle ECB$. 在$\triangle AEF$和$\triangle CEB$中,$\left\{\begin{array}{l} \angle AEF=\angle CEB=90^{\circ},\\ AE=CE,\\ \angle EAF=\angle ECB,\end{array}\right.\therefore \triangle AEF\cong \triangle CEB(ASA)$.
(2)$\because \triangle AEF\cong \triangle CEB,\therefore AF=BC$. $\because AB=AC,AD\perp BC,\therefore BD=CD,\therefore AF=BC=2CD$.
1. 在$\triangle ABC$中,$\angle B= \angle C$,$AB = 5$,则$AC$的长为( )
A.12
B.9
C.5
D.2
A.12
B.9
C.5
D.2
答案:
C
2. 如图1,在$\triangle ABC$中,$\angle A = 36^{\circ}$,$AB = AC$,点$D在边AC$上,$\triangle BCD沿着BD$对折,点$C的对称点E恰好边AB$上,则图中等腰三角形共有( ).
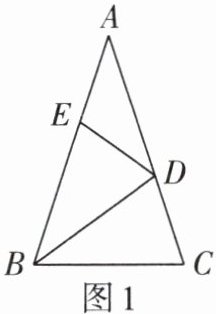
A.2个
B.3个
C.4个
D.5个

A.2个
B.3个
C.4个
D.5个
答案:
D
3. 如图2,给出了尺规作等腰三角形的三种作法,认真观察作图痕迹,下面的“已知”分别对应作图顺序正确的是( )
①已知等腰三角形的底边和底边上的高; ②已知等腰三角形的底边和腰;
③已知等腰三角形的底边和一底角.
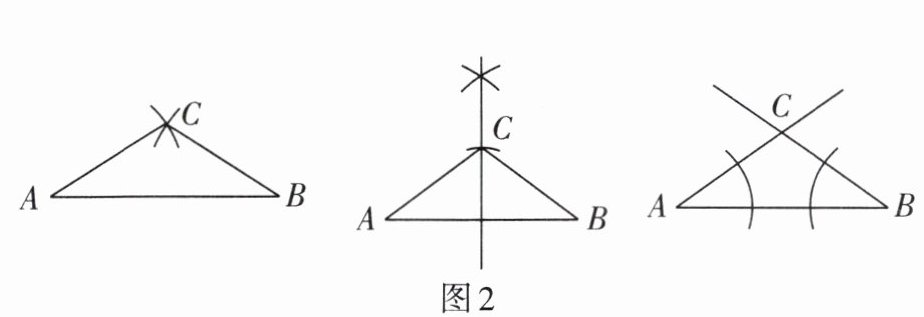
A.①②③
B.②①③
C.③①②
D.②③①
①已知等腰三角形的底边和底边上的高; ②已知等腰三角形的底边和腰;
③已知等腰三角形的底边和一底角.

A.①②③
B.②①③
C.③①②
D.②③①
答案:
B
查看更多完整答案,请扫码查看


