《2025年新课程课堂同步练习册八年级数学上册人教版》

4. 如图2,已知$\triangle ABC\cong\triangle ADE$,点$D在BC$上.若$\angle CAE = 40^{\circ}$,则$\angle B$的度数是( )


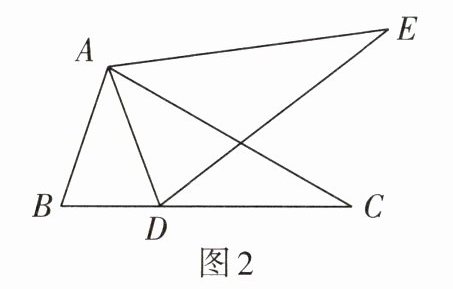
A.$70^{\circ}$
B.$68^{\circ}$
C.$65^{\circ}$
D.$60^{\circ}$

答案： A

5. 如图3,在$\triangle ABC$中,$PM$,$QN分别是线段AB$,$AC$的垂直平分线.若$\angle BAC = 110^{\circ}$,则$\angle PAQ$的度数是( )


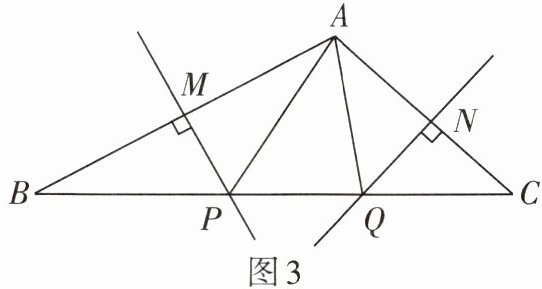
A.$30^{\circ}$
B.$40^{\circ}$

C.$50^{\circ}$
D.$70^{\circ}$

答案： B

1. 如图4,在$\triangle ABC$中,$AB = AC$,$D是边BC$的中点.连接$AD$,若$\angle ABC = 50^{\circ}$,则$\angle BAD$的度数为______.

答案： $40^{\circ}$

2. 如图5,已知$AB = AC$,$AD = AE$.若$BE = 8$,$DE = 2$,则$BC = $______.

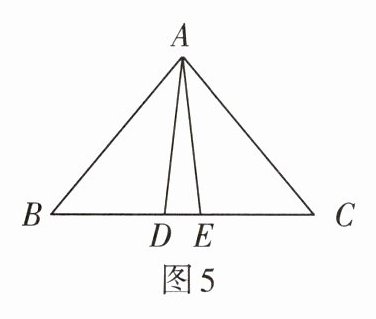
答案： 14

3. 如图6 - 1所示的“三等分角仪”能三等分任意一个角.这个三等分角仪由两根有槽的棒$OA$,$OB$组成,两根棒在$O点相连并可绕O$点转动.$C$点固定,$OC = CD = DE$,点$D$,$E$可在槽中滑动.如图6 - 2,若$\angle BDE = 84^{\circ}$,则$\angle CDE$的度数是______。

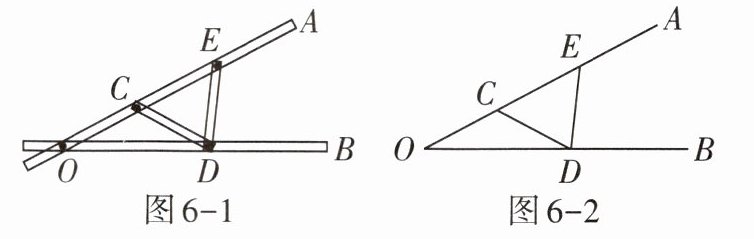
答案： $68^{\circ}$

4. 如图7,直线$BD\perp AC$,垂足为点$O$,且$AO = CO$.若$\angle ADC + \angle ABC = 220^{\circ}$,则$\angle DAB$的度数为______.

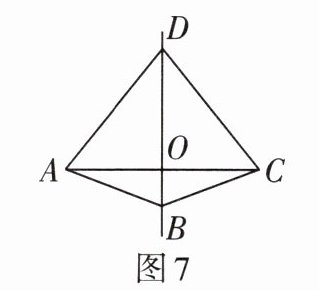
答案： $70^{\circ}$

1. 如图8,在$\triangle ABD$中,$AB = AC = DC$,$\angle BAC = 40^{\circ}$,求$\angle BAD$的度数.

答案： $\because AB=AC=DC,\therefore \angle B=\angle ACB,\angle D=\angle CAD$. $\because \angle BAC=40^{\circ},\therefore \angle ACB=\frac{1}{2}(180^{\circ}-\angle BAC)=\frac{1}{2}(180^{\circ}-40^{\circ})=70^{\circ}$. $\because \angle ACB=\angle D+\angle CAD=2\angle CAD$, $\therefore 2\angle CAD=70^{\circ},\therefore \angle CAD=35^{\circ},\therefore \angle BAD=\angle BAC+\angle CAD=40^{\circ}+35^{\circ}=75^{\circ}$.