《2025年新课程课堂同步练习册八年级数学上册人教版》

4. 如图 9,在 $ \triangle ABC $ 中,点 $ D,E $ 分别在 $ BC,AB $ 上, $ AD $ 交 $ CE $ 于点 $ F $ 。
(1)写出以 $ \angle ADC $ 为内角的三角形。
(2)写出 $ \angle ACF $ 的对边。
(3)写出以线段 $ BC $ 为边的三角形。

答案：
(1)含有∠ADC的三角形有△ADC,△DCF.
(2)在△ACF中,∠ACF的对边是AF;在△ACE中,∠ACF的对边是AE.
(3)以线段BC为边的三角形有△ABC,△BCE.

1. 以下列各组线段为边能构成三角形的是( )

A.$3\mathrm{cm},2\mathrm{cm},5\mathrm{cm}$
B.$7\mathrm{cm},3\mathrm{cm},3\mathrm{cm}$
C.$4\mathrm{cm},5\mathrm{cm},6\mathrm{cm}$
D.$8\mathrm{cm},10\mathrm{cm},20\mathrm{cm}$

答案： C

2. 已知三角形的两边长分别为$4\mathrm{cm}和9\mathrm{cm}$,则下列长度的四条线段中能作为第三边的是( )

A.$13\mathrm{cm}$
B.$6\mathrm{cm}$
C.$5\mathrm{cm}$
D.$4\mathrm{cm}$

答案： B

3. 已知等腰三角形的两条边长分别为$4\mathrm{cm}和9\mathrm{cm}$,则它的周长为( )

A.$17\mathrm{cm}$
B.$22\mathrm{cm}$
C.$19\mathrm{cm}$
D.$17\mathrm{cm}或22\mathrm{cm}$

答案： B

4. 三条线段的长度比如下,不能组成三角形的是( )

A.$1:2:3$
B.$2:3:4$
C.$3:4:5$
D.$4:5:6$

答案： A

5. 已知三角形三边长分别为$2,x,13$,若$x$为正整数,则这样的三角形个数为( )

A.$2$
B.$3$
C.$5$
D.$7$

答案： B

1. 如图1,工人师傅砌门时,常用木条$EF固定长方形门框ABCD$,使其不变形,这种做法的依据是 。

答案： 三角形具有稳定性

2. 如图2,在$\triangle ABC$中,有$AB + AC$ $BC$(填“$＞$”“$＜$”或“$=$”),理由是 ,这个结论是由基本事实 得到的。

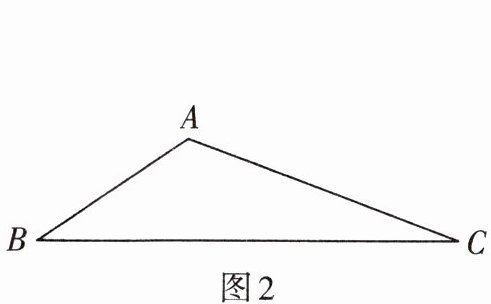
答案： ＞,三角形两边的和大于第三边,两点之间线段最短