《2025年新课程课堂同步练习册八年级数学上册人教版》

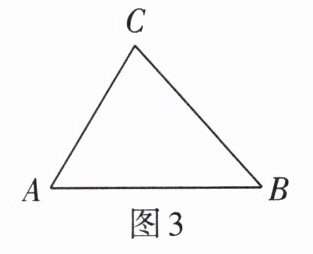
3. 三条公路将$A$、$B$、$C$三个村庄连成一个如图3所示的三角形区域,如果在这个区域内修建一个集贸市场,要使集贸市场到三条公路的距离相等,那么这个集贸市场应建的位置是( )


A.三条高线的交点
B.三条中线的交点
C.三条角平分线的交点
D.不确定

答案： C

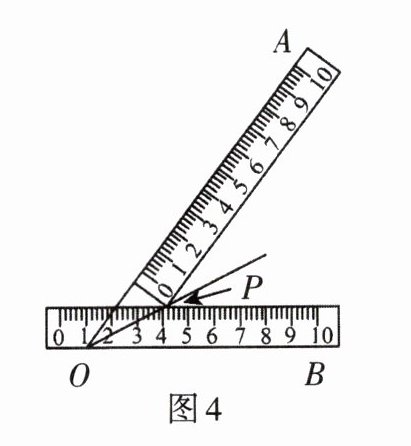
4. 小明同学只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图4,一把直尺压住射线$OB$,另一把直尺压住射线$OA并且与第一把直尺交于点P$.小明说：“射线$OP就是\angle BOA$的角平分线.”他这样做的依据是( )


A.在角的内部,到角的两边距离相等的点在角的平分线上
B.角平分线上的点到这个角两边的距离相等
C.三角形的三条角平分线交于一点
D.三角形三边的垂直平分线交于一点

答案： A

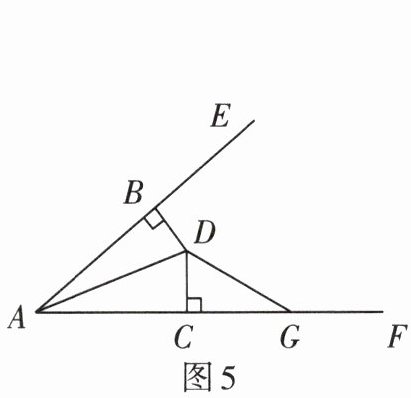
5. 如图5,已知$BD\perp AE于点B$,$DC\perp AF于点C$,且$DB = DC$,$\angle BAC = 40^{\circ}$,$\angle ADG = 130^{\circ}$,则$\angle CDG$的度数为( )


A.$30^{\circ}$

B.$40^{\circ}$
C.$50^{\circ}$
D.$60^{\circ}$

答案： D

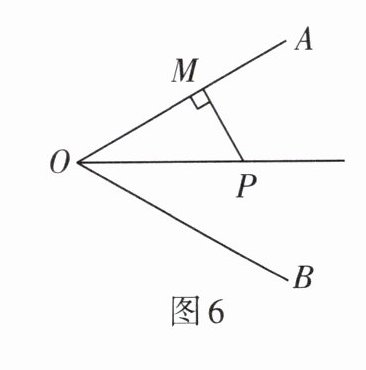
1. 如图6,$PM\perp OA$,$PM = 1$,当点$P到OB$的距离为______时,$\angle POA = \angle POB$.

答案： 1

2. 如图7,已知$\angle CDA = \angle CBA = 90^{\circ}$,且$CD = CB$,则点$C在\angle$______的平分线上,点$A在\angle$______的平分线上.

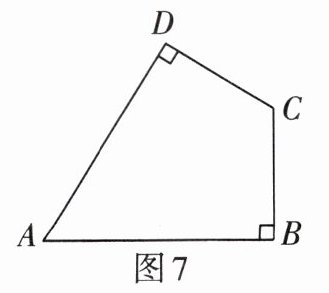
答案： BAD,BCD

3. 如图8,已知点$P到\triangle ABC$三边的距离相等,$\angle B = 80^{\circ}$,则$\angle P = $______.

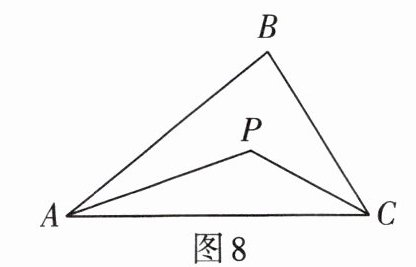
答案： 130°

4. 如图9,在$\triangle ABC$中,$\angle CAB = 50^{\circ}$,点$D在\triangle ABC$的外部,且$AD平分\angle BAC$,过点$D作DE\perp AC$,交$AC的延长线于点E$,$DF\perp BC$,交$BC于点F$,连接$BD$.若$\angle BCE = 104^{\circ}$,$DE = DF$,则$\angle DBC$的度数为______.

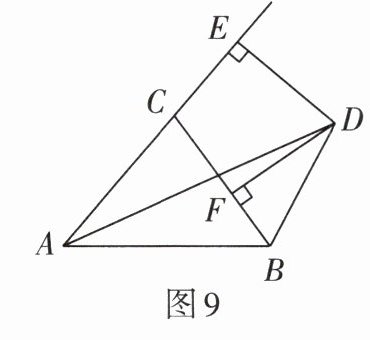
答案： 63°