《2025年新课程课堂同步练习册八年级数学上册人教版》

4. 如图 4,在$\triangle ABC$中,点$D在AC$上,点$E在BC$上,连接$BD$,$DE$. 若$AB = EB$,$AD = ED$,$\angle A = 80^{\circ}$,$\angle BDC = 110^{\circ}$,则$\angle C$的度数为( )

A.$30^{\circ}$

B.$40^{\circ}$
C.$45^{\circ}$
D.$50^{\circ}$

答案： B

1. 如图 5,若$AB = DE$,$AC = DF$,$BC = EF$,则$\angle E = $______.

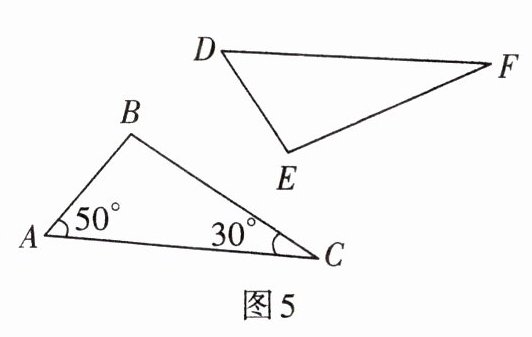
答案： 100°

2. 如图 6,$AB = AC$,$BE = CD$,要使$\triangle ABE \cong \triangle ACD$,依据$SSS$,则还需添加条件______. (填一个即可)

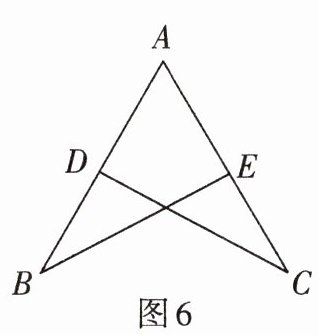
答案： AE=AD或CE=BD(填其中任一个均可)

3. 如图 7,在$\triangle ABC和\triangle BDE$中,点$C在边BD$上,$AC交BE于点F$. 若$AC = BD$,$AB = ED$,$BC = BE$,$\angle ACB = 50^{\circ}$,则$\angle AFB = $______.

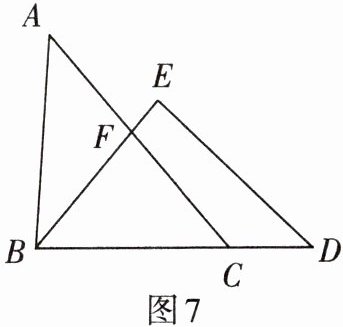
答案： 100°

4. 一个三角形的三边长为$5$,$x$,$14$,另一个三角形的三边长为$5$,$10$,$y$,若由“$SSS$”可以判定这两个三角形全等,则$x + y = $______.

答案： 24

1. 如图 8,点$G$,$E在BC$上,$BG = CE$,$AB = DC$,$AE = DG$. 求证：$\angle B = \angle C$.

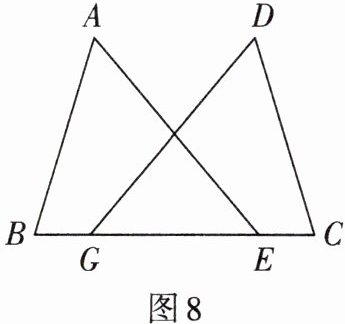
答案： 提示:证△ABE≌△DCG.

2. 如图 9,$\triangle ABC$是一个“人”字型的钢架,$AB = AC$,$AD是连接点A与BC中点D$的支架. 求证：$AD \perp BC$.

答案： 提示:先证△ABD≌△ACD,再证∠ADB=90°.