《2025年新课程课堂同步练习册八年级数学上册人教版》

4. 用悬挂法测重心时,两次悬挂线的交点即为重心. 其原理是( )

A.重心到悬挂点的距离相等
B.重心在悬线的延长线上
C.重心受到的拉力最大
D.悬线方向与重力方向垂直

答案： B

1. 如图3,嘉嘉用细线绑一块木板,然后提着细线使木板悬空. 嘉嘉发现,当将细线在A,C处捆绑木板时,木板不能水平悬空,而将细线在B处捆绑时,木板能水平悬空,则可以确定木板的重心在______处.

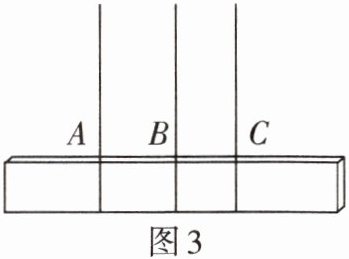
答案： B

2. 一块匀质三角形薄板的三个顶点坐标为A(0,0),B(4,0),C(0,3),其重心坐标为______.

答案： $\left(\dfrac{4}{3},1\right)$

3. 如图4,在平面直角坐标系内构造出小正方形的边长均为单位长1的8×4网格,且点A,B,C都是格点,则△ABC的重心坐标为______.

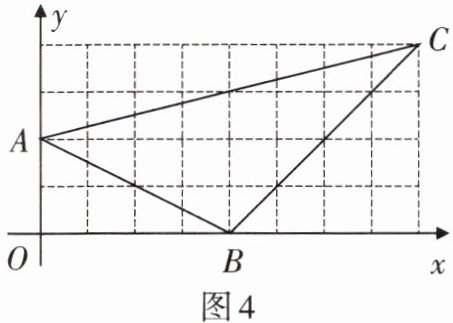
答案： $(4,2)$

1. 小敏同学利用作图法找出如图5所示均匀薄铁片的重心,他把整块铁片分成两个长方形,确定它们的重心$O_1,O_2,$那么整个铁片的重心必在$O_1,O_2$的连线上. 请利用这个思路和作法,找出铁片的重心.

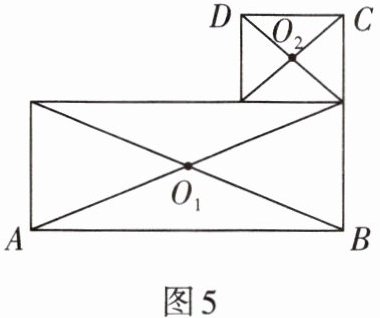
答案： 如图1,把铁片重新分成另两个长方形,并确定它们的重心$O_{3},O_{4}$,那么重心也必在$O_{3}O_{4}$上,则$O_{1}O_{2}$与$O_{3}O_{4}$的交点即为该铁片的重心$O$.

2. 某艺术工作室设计了一款“T”形装饰薄板,其尺寸如图6所示(单位：cm),薄板材质均匀,且上下长方形左右对称分布,请计算该“T”形装饰薄板的重心位置.

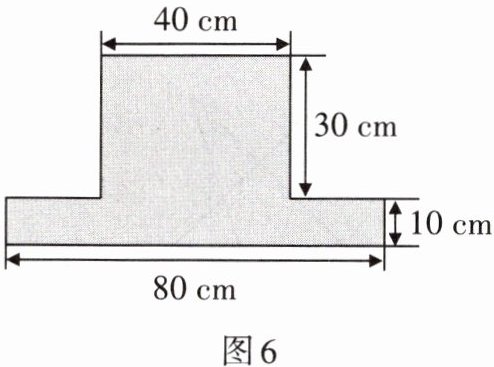
答案： 把“T”形装饰薄板分割成两个矩形,矩形1的面积为$S_{1}=80×10=800({cm}^{2})$,矩形2的面积为$S_{2}=40×30=1200({cm}^{2})$,总面积$S=800\ {cm}^{2}+1200\ {cm}^{2}=2000\ {cm}^{2}$. 以图形左下角为坐标原点建立平面直角坐标系,如图2所示. 对于矩形1,其重心坐标$(x_{1},y_{1})$,$x_{1}=\dfrac{80}{2}=40$,$y_{1}=\dfrac{10}{2}=5$;对于矩形2,其重心坐标$(x_{2},y_{2})$,$x_{2}=\dfrac{80}{2}=40$,$y_{2}=10+\dfrac{30}{2}=25$. 根据重心坐标公式得“T”形板的重心坐标$(x,y)$,$x=\dfrac{S_{1}x_{1}+S_{2}x_{2}}{S}=\dfrac{800×40+1200×40}{2000}=40$,$y=\dfrac{S_{1}y_{1}+S_{2}y_{2}}{S}=\dfrac{800×5+1200×25}{2000}=17$,$\therefore$该“T”形装饰薄板的重心位置为$(40,17)$.