《2025年新课程课堂同步练习册八年级数学上册人教版》

3. 如图9,在Rt△ABC中,CM平分∠ACB,交AB于点M,过点M作MN//BC交AC于点N,且MN平分∠AMC,若AN= 1,则BC的长是多少？

答案： $BC=6$. 提示:先证$\angle ACB=2\angle B$,再证$\angle B=30°$.

1. 直线 $ a $ 是一条输气管道,$ M $,$ N $ 是管道同侧的两个村庄,现计划在直线 $ a $ 上修建一个供气站 $ O $,向 $ M $,$ N $ 两村庄供应天然气。在下列图的四种方案中,铺设管道最短的是( )

答案： C

2. 直线 $ l_1 $,$ l_2 $ 表示一条河的两岸,且 $ l_1 // l_2 $,若村庄 $ P $ 和村庄 $ Q $ 在这条河的两岸。现要在这条河上建一座桥 $ EF $(桥 $ EF $ 与河的两岸 $ l_1 $,$ l_2 $ 垂直),使得从村庄 $ P $ 经桥 $ EF $ 过河到村庄 $ Q $ 的路径 $ PEFQ $ 最短,即 $ PE + EF + FQ $ 最小,则下列图中满足条件的是( )

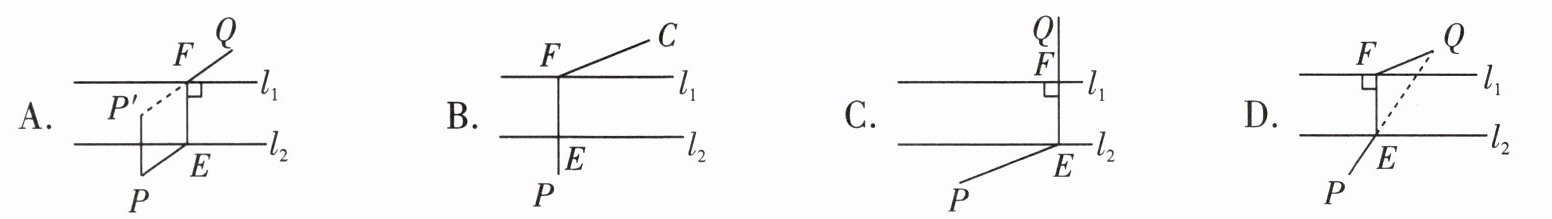
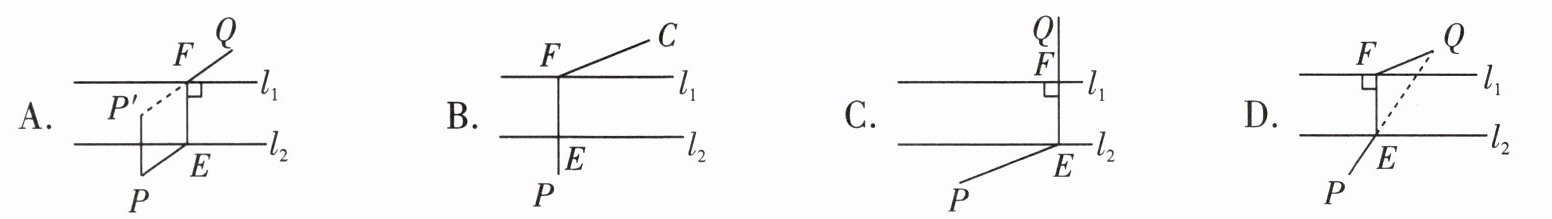
答案： A

3. 如图 1,在 $ \triangle ABC $ 中,$ AB = 3 $,$ AC = 4 $,$ EF $ 垂直平分 $ BC $,交 $ AC $ 于点 $ D $,则 $ \triangle ABP $ 周长的最小值是( )


A.12
B.6
C.7
D.8

答案： C

4. 如图 2,在等边 $ \triangle ABC $ 中,$ BC $ 边上的高 $ AD = 8 $,$ E $ 是高 $ AD $ 上的一个动点,$ F $ 是边 $ AB $ 的中点,在点 $ E $ 运动的过程中,存在 $ EB + EF $ 的最小值,则这个最小值是( )


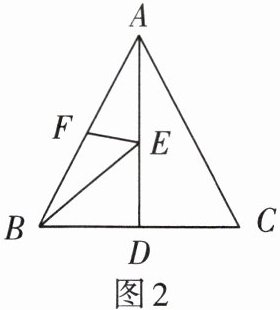
A.5

B.6
C.7
D.8

答案： D