第33页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
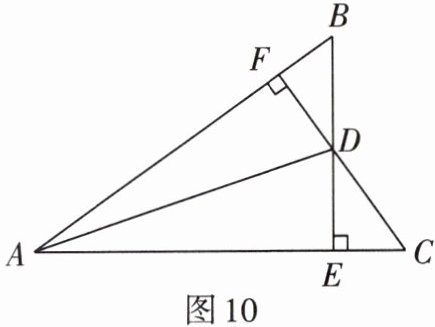
1. 如图10,已知$BE\perp AC于E$,$CF\perp AB于F$,$BE$,$CF相交于点D$,且$BD = CD$.求证:$AD平分\angle BAC$.

答案:
证明:
∵BE⊥AC,CF⊥AB,
∴∠DFB=∠DEC=90°. 又
∵∠FDB=∠EDC,BD=CD,
∴△FBD≌△ECD(AAS),
∴DF=DE. 又
∵BE⊥AC,CF⊥AB,
∴AD平分∠BAC.
∵BE⊥AC,CF⊥AB,
∴∠DFB=∠DEC=90°. 又
∵∠FDB=∠EDC,BD=CD,
∴△FBD≌△ECD(AAS),
∴DF=DE. 又
∵BE⊥AC,CF⊥AB,
∴AD平分∠BAC.
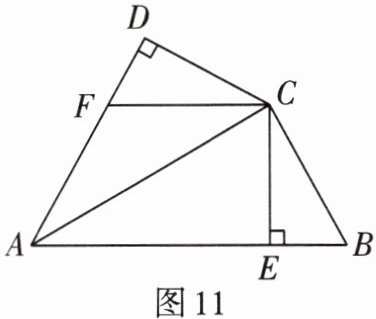
2. 如图11,已知$BE = FD$,$CE\perp AB于点E$,$CD\perp AF交AF的延长线于点D$,且$BC = FC$.求证:$AC是\angle BAF$的平分线.

答案:
证明:
∵CE⊥AB,CD⊥AF,
∴∠CEB=∠D=90°. 在Rt△BCE和Rt△FCD中,{BC=FC,BE=FD},
∴Rt△BCE≌Rt△FCD(HL),
∴CE=CD.
∵CE⊥AB,CD⊥AF,
∴点C在∠BAF的平分线上,
∴AC是∠BAF的平分线.
∵CE⊥AB,CD⊥AF,
∴∠CEB=∠D=90°. 在Rt△BCE和Rt△FCD中,{BC=FC,BE=FD},
∴Rt△BCE≌Rt△FCD(HL),
∴CE=CD.
∵CE⊥AB,CD⊥AF,
∴点C在∠BAF的平分线上,
∴AC是∠BAF的平分线.
3. 【课本再现】
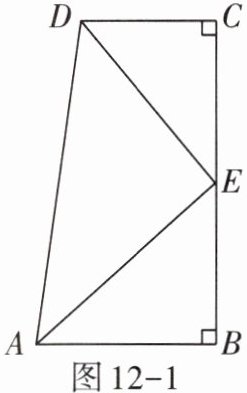
(1)如图12-1,$\angle B = \angle C = 90^{\circ}$,$E是BC$的中点,$DE平分\angle ADC$.求证:$AE是\angle BAD$的平分线.
【变式探究】
(2)如图12-2,$AB// CD$,$AE是\angle BAD$的平分线,$DE是\angle ADC$的平分线.
①求证:$\angle AED = 90^{\circ}$;
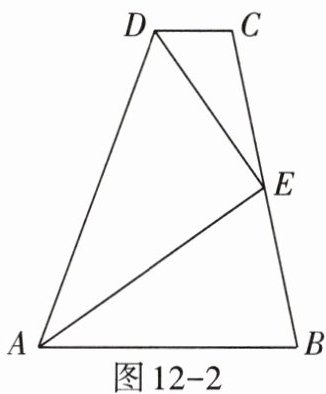
②求证:$AD = AB + CD$.
(1)如图12-1,$\angle B = \angle C = 90^{\circ}$,$E是BC$的中点,$DE平分\angle ADC$.求证:$AE是\angle BAD$的平分线.
【变式探究】
(2)如图12-2,$AB// CD$,$AE是\angle BAD$的平分线,$DE是\angle ADC$的平分线.
①求证:$\angle AED = 90^{\circ}$;


②求证:$AD = AB + CD$.
答案:
证明:
(1)如图1,过点E作EF⊥DA于点F,
∵DE平分∠ADC,∠C=90°,即EC⊥CD,
∴CE=EF.
∵E是BC的中点,
∴BE=CE,
∴BE=EF.又
∵∠B=90°,EF⊥DA,点E在∠BAD的内部,
∴AE平分∠BAD.
(2)①
∵AB//CD,
∴∠BAD+∠ADC=180°.
∵AE是∠BAD的平分线,DE是∠ADC的平分线,
∴∠BAE=∠DAE=1/2∠BAD,∠ADE=∠CDE=1/2∠ADC,
∴∠ADE+∠DAE=1/2∠ADC+1/2∠BAD=1/2(∠ADC+∠BAD)=90°,
∴∠AED=180°-(∠ADE+∠DAE)=90°. ②如图2,在AD上截取DF=DC,连接EF.
∵AE是∠BAD的平分线,DE是∠ADC的平分线,
∴∠BAE=∠FAE,∠FDE=∠CDE. 在△CDE和△FDE中,{DC=DF,∠CDE=∠FDE,DE=DE,}
∴△CDE≌△FDE(SAS),
∴∠CED=∠FED. 由①已证:∠AED=90°,
∴∠CED+∠AEB=180°-∠AED=90°,∠FED+∠AEF=∠AED=90°,
∴∠AEB=∠AEF. 在△AEB和△AEF中,{∠AEB=∠AEF,AE=AE,∠BAE=∠FAE},
∴△AEB≌△AEF(ASA),
∴AF=AB,
∴AD=AF+DF=AB+CD.
(1)如图1,过点E作EF⊥DA于点F,
∵DE平分∠ADC,∠C=90°,即EC⊥CD,
∴CE=EF.
∵E是BC的中点,
∴BE=CE,
∴BE=EF.又
∵∠B=90°,EF⊥DA,点E在∠BAD的内部,
∴AE平分∠BAD.
(2)①
∵AB//CD,
∴∠BAD+∠ADC=180°.
∵AE是∠BAD的平分线,DE是∠ADC的平分线,
∴∠BAE=∠DAE=1/2∠BAD,∠ADE=∠CDE=1/2∠ADC,
∴∠ADE+∠DAE=1/2∠ADC+1/2∠BAD=1/2(∠ADC+∠BAD)=90°,
∴∠AED=180°-(∠ADE+∠DAE)=90°. ②如图2,在AD上截取DF=DC,连接EF.
∵AE是∠BAD的平分线,DE是∠ADC的平分线,
∴∠BAE=∠FAE,∠FDE=∠CDE. 在△CDE和△FDE中,{DC=DF,∠CDE=∠FDE,DE=DE,}
∴△CDE≌△FDE(SAS),
∴∠CED=∠FED. 由①已证:∠AED=90°,
∴∠CED+∠AEB=180°-∠AED=90°,∠FED+∠AEF=∠AED=90°,
∴∠AEB=∠AEF. 在△AEB和△AEF中,{∠AEB=∠AEF,AE=AE,∠BAE=∠FAE},
∴△AEB≌△AEF(ASA),
∴AF=AB,
∴AD=AF+DF=AB+CD.
查看更多完整答案,请扫码查看


