《2025年新课程课堂同步练习册八年级数学上册人教版》

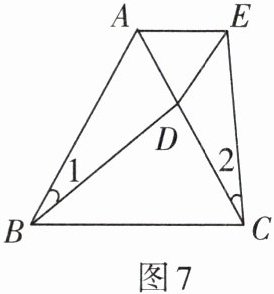
3. 如图7,$\triangle ABC$为等边三角形,$\angle 1= \angle 2$,$BD = CE$. 求证:$\triangle ADE$是等边三角形.

答案： 解：
因为$\triangle ABC$是等边三角形，所以$AB = AC$，$\angle BAC=60^{\circ}$。
在$\triangle ABD$和$\triangle ACE$中，$\begin{cases}AB = AC\\\angle 1=\angle 2\\BD = CE\end{cases}$，根据$SAS$（边角边）定理可得$\triangle ABD\cong\triangle ACE$。
所以$AD = AE$，$\angle BAD=\angle DAE=60°$。
因为$AD = AE$，$\angle DAE = 60^{\circ}$，根据有一个角是$60^{\circ}$的等腰三角形是等边三角形，所以$\triangle ADE$是等边三角形。

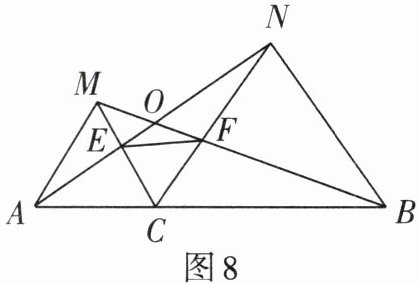
4. 如图8,已知点$C为线段AB$上一点,$\triangle ACM$,$\triangle CBN$都是等边三角形,$AN交MC于点E$,$BM交CN于点F$.
(1)求证:$AN = BM$;
(2)求$AN与BM$相交所成锐角的大小;
(3)求证:$\triangle CEF$为等边三角形.

答案：
(1)提示:证△ACN≌△MCB(SAS),
∴AN=BM.
(2)由
(1)得△ACN≌△MCB,
∴∠CAN=∠CMB. 由题图可知,此题为求∠AOM的大小. ∠MOA=180°-∠MAO-∠AMO=180°-∠MAO-∠AMC-∠CMB=180°-∠MAO-60°-∠CAN=120°-(∠MAO+∠CAN)=120°-∠MAC=120°-60°=60°. 即AN与BM相交所成锐角为60°.
(3)
∵∠CAE=∠CMF,CA=CM,∠ACE=∠MCF,
∴△CAE≌△CMF(ASA),
∴CE=CF,
∴△CEF为等腰三角形. 又
∵∠ECF=60°,
∴△CEF为等边三角形.

1. 在△ABC中,∠A∶∠B∶∠C= 1∶2∶3,则BC∶AB等于( )

A.2∶1
B.1∶2
C.1∶3
D.2∶3

答案： B

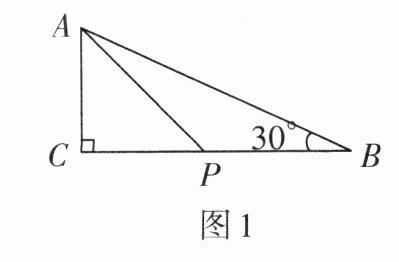
2. 如图1,在△ABC中,∠C= 90°,AC= 3,∠B= 30°,点P是BC边上的动点,则AP的长不可能是( )


A.3.5
B.4.2
C.5.8
D.7

答案： D

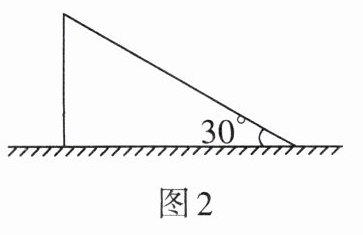
3. 如图2,一棵树在一次强台风中于离地面3米处折断倒下,倒下部分与地面成30°角,这棵树在折断前的高度为( )


A.6米
B.9米
C.12米
D.15米

答案： B