《2025年新课程课堂同步练习册八年级数学上册人教版》

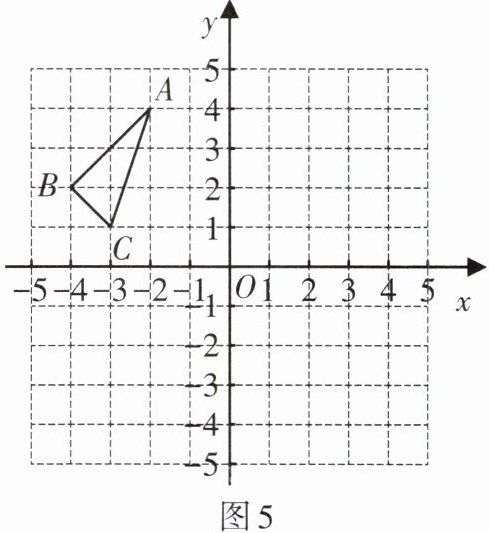
2. $\triangle ABC$在平面直角坐标系中的位置如图5所示,其中$A(-2,4)$,$B(-4,2)$,$C(-3,1)$,每个小正方形的边长为$1$个单位长度.
(1)$\triangle ABC关于y轴对称图形为\triangle A_{1}B_{1}C_{1}$,画出$\triangle A_{1}B_{1}C_{1}$的图形,并写出$A_{1}$,$B_{1}$,$C_{1}$三点的坐标：$A_{1}$(______,______),$B_{1}$(______,______),$C_{1}$(______,______).
(2)计算$\triangle ABC$的面积.

答案：
(1)如图1所示,△A₁B₁C₁即为所求. A₁(2,4),B₁(4,2),C₁(3,1)
(2)S△ABC=2×3-$\frac {1}{2}$×1×1-$\frac {1}{2}$×1×3-$\frac {1}{2}$×2×2=6-$\frac {1}{2}$-$\frac {3}{2}$-2=2.

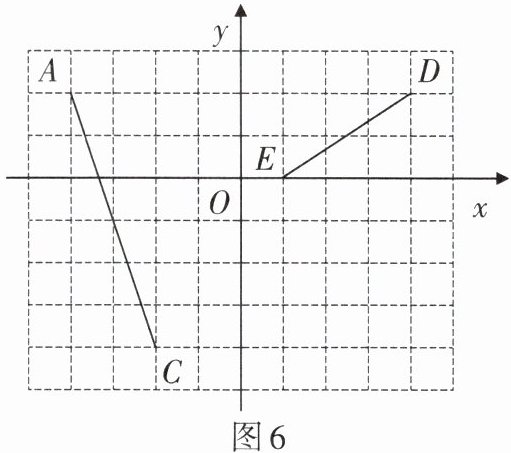
3. 如图6,在平面直角坐标系中,$\triangle ABC$的顶点均在正方形网格的格点上,且点$A的坐标为(-4,2)$,$\triangle DEF和\triangle ABC关于y$轴对称(点$A$,$B的对应点分别为点D$,$E$).
(1)在图中把$\triangle ABC和\triangle DEF$补充完整；
(2)计算$\triangle ABC$的面积.

答案：
(1)
∵点B和E(1,0)关于y轴对称,点C(-2,-4)和F关于y轴对称,
∴B(-1,0),F(2,-4),把△ABC和△DEF补充完整如图2所示.
(2)如图2,分别过点A、C作x轴的平行线,分别过点A、B作y轴的平行线,交点为G、H、M.
∴S△ABC=S长方形AGHM-S△ABG-S△BCH-S△ACM=AG·AM-$\frac {1}{2}$AG·BG-$\frac {1}{2}$CH·BH-$\frac {1}{2}$CM·AM=3×6-$\frac {1}{2}$×3×2-$\frac {1}{2}$×1×4-$\frac {1}{2}$×2×6=18-3-2-6=7,
∴△ABC的面积为7.

1. 若等腰三角形的顶角为$36^{\circ}$,则底角为( )

A.$36^{\circ}$
B.$54^{\circ}$
C.$72^{\circ}$
D.$108^{\circ}$

答案： C

2. 如果等腰三角形两边长是$2\mathrm{cm}和4\mathrm{cm}$,那么它的周长是( )

A.$8\mathrm{cm}$
B.$10\mathrm{cm}$
C.$8\mathrm{cm}或10\mathrm{cm}$
D.$12\mathrm{cm}$

答案： B

3. 如图1,在$\triangle ABC$中,$AB = AC$,$D是BC$的中点,下列结论中,不正确的是( )

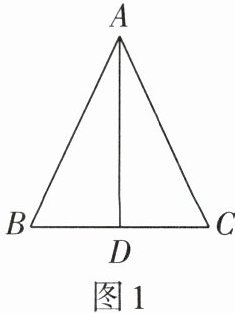
A.$AB = 2BD$
B.$AD\perp BC$
C.$AD平分\angle BAC$
D.$\angle B= \angle C$

答案： A