《2025年新课程课堂同步练习册八年级数学上册人教版》

3. 如图9,在$\triangle ABC$中,$\angle BAC= 90^{\circ}$,$AB= AC$,直线$m经过点A$,$BD\perp m$,$CE\perp m$,垂足分别为点$D$,$E$。
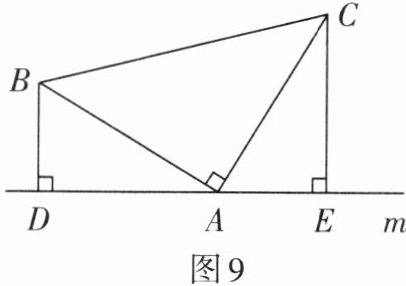
求证：(1)$\triangle BDA\cong\triangle AEC$；(2)$DE= BD+CE$。

答案： 提示:
(1)由$BD⊥m,CE⊥m$,证$∠ADB=∠CEA=90^{\circ }$,则$∠ABD+∠BAD=90^{\circ }$,由$∠BAC=90^{\circ }$,可证$∠BAD+∠CAE=90^{\circ }$,则$∠ABD=∠CAE$,又$AB=AC$,可证得$△BDA\cong △AEC$.
(2)由$△BDA\cong △AEC$,可得$BD=AE,AD=CE$,可证得$DE=DA+AE=BD+CE$.

4. 如图10,在$\triangle ABC$中,$D是边AB$上一点,$E是边AC$的中点,作$CF// AB交DE的延长线于点F$。
(1)求证：$\triangle ADE\cong\triangle CFE$；
(2)若$AB= AC$,$CE= 6$,$CF= 8$,求$DB$的长。

答案： 提示:
(1)根据点E是边AC的中点,得出$AE=CE$,又$CF// AB$,再根据平行线的性质得出$∠A=∠ACF,∠ADE=∠F$,即可证明$△ADE\cong △CFE$.
(2)根据$△ADE\cong △CFE$得出$CF=AD=8$,进而得出$AB=AC=2CE=12$,根据线段的和差得出$DB=AB-AD=12-8=4$.

1. 如图 1,$AB = AD$,$CB = CD$,$\angle B = 30^{\circ}$,$\angle BAD = 46^{\circ}$,则$\angle ACD$的度数是( )


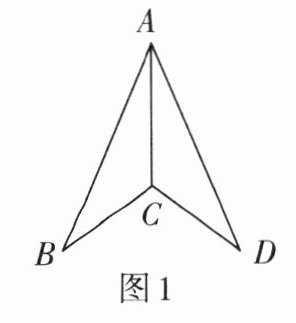
A.$120^{\circ}$
B.$125^{\circ}$
C.$127^{\circ}$
D.$104^{\circ}$

答案： C

2. 如图 2,已知$AB = DC$,若用定理$SSS证明\triangle ABC \cong \triangle DCB$,则需要添加的条件是( )


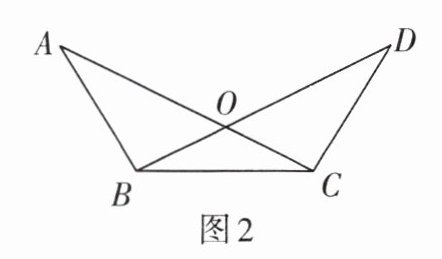
A.$OA = OD$
B.$AC = DB$
C.$OB = OC$
D.$BC = CB$

答案： B

3. 我国传统工艺中,油纸伞制作非常巧妙,其中蕴含着数学知识. 如图 3 是油纸伞的张开示意图,$AE = AF$,$GE = GF$,则$\triangle AEG \cong \triangle AFG$的依据是( )


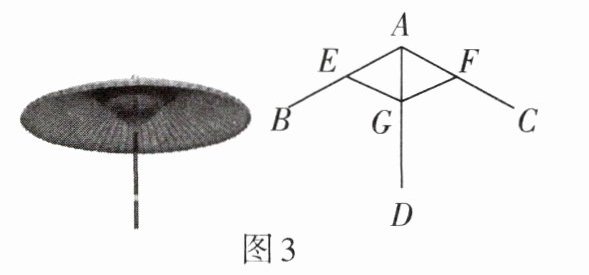
A.$SAS$

B.$ASA$
C.$AAS$
D.$SSS$

答案： D