《2025年新课程课堂同步练习册八年级数学上册人教版》

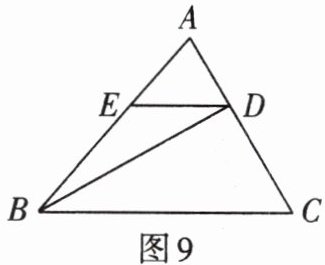
3. 如图 9,在 $ \triangle ABC $ 中, $ \angle A = 70^{\circ} $, $ \angle ABC = 50^{\circ} $.
(1)求 $ \angle C $ 的度数;
(2)若 $ \angle BDE = 30^{\circ} $, $ DE // BC $ 交 $ AB $ 于点 $ E $,判断 $ \triangle BDC $ 的形状,并说明理由.

答案：
(1)$\because \angle A=70^{\circ},\angle ABC=50^{\circ},\therefore \angle C=180^{\circ}-\angle A-\angle ABC=180^{\circ}-70^{\circ}-50^{\circ}=60^{\circ}$.
(2)$\triangle BDC$为直角三角形. 理由如下:$\because DE// BC,\therefore \angle CBD=\angle BDE=30^{\circ}$,由
(1)得$\angle C=60^{\circ},\therefore \angle BDC=180^{\circ}-\angle CBD-\angle C=180^{\circ}-30^{\circ}-60^{\circ}=90^{\circ},\therefore \triangle BDC$为直角三角形.

4. 如图, $ CD $ 是 $ \triangle ABC $ 的角平分线,点 $ E $ 在 $ AC $ 上, $ BE $ 交 $ CD $ 于点 $ F $, $ \angle ACB = 56^{\circ} $.
(1)如图 10 - 1,若 $ BE \perp AC $,求 $ \angle DFB $ 的度数;
(2)如图 10 - 2,若 $ BE \perp CD $, $ \angle A = 50^{\circ} $,求 $ \angle ABE $ 的度数.

答案：
(1)$\because CD$是$\angle ACB$的平分线,$\therefore \angle ACD=\frac{1}{2}\angle ACB=28^{\circ}$. $\because BE\perp AC,\therefore \angle CEF=90^{\circ}$.在$Rt\triangle CEF$中,$\angle EFC=90^{\circ}-\angle ACD=90^{\circ}-28^{\circ}=62^{\circ},\therefore \angle DFB=\angle EFC=62^{\circ}$.
(2)$\because BE\perp CD,\therefore \angle EFC=90^{\circ}$. 又由
(1)知$\angle ECF=28^{\circ},\therefore \angle CEB=90^{\circ}-\angle ECF=90^{\circ}-28^{\circ}=62^{\circ},\therefore \angle ABE=\angle CEB-\angle A=62^{\circ}-50^{\circ}=12^{\circ}$.

1. 如图1,下列说法错误的是( )


A.∠EFD是△BFC的一个外角
B.∠DFC是△BFC的一个外角
C.∠EFD+∠FBC+∠FCB= 180°
D.∠CDF= ∠A+∠ABD

答案： A

2. 如图2,∠1,∠2,∠3的大小关系为( )


A.∠2＞∠1＞∠3

B.∠1＞∠3＞∠2
C.∠3＞∠2＞∠1
D.∠1＞∠2＞∠3

答案： D