《2025年新课程课堂同步练习册八年级数学上册人教版》

1. 判定两个直角三角形全等的条件可以是( )

A.一锐角对应相等
B.两锐角对应相等
C.一条边对应相等
D.两条直角边对应相等

答案： D

2. 如图1,在△ABC中,AD⊥BC,若要根据“HL”来证明△ADB≌△ADC,则需要补充的一个条件是( )


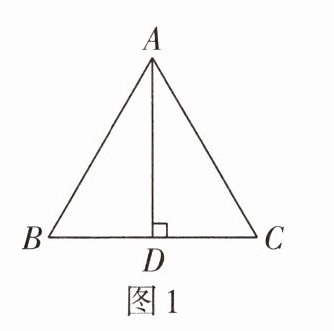
A.AD= AD
B.BD= CD
C.AB= AC
D.∠B= ∠C

答案： C

3. 如图2,BE⊥AC于点D,且AD= CD,BD= ED,若∠ABC= 54°,则∠E的度数为( )


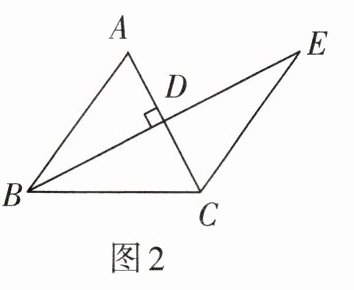
A.25°
B.27°
C.30°
D.45°

答案： B

4. 如图3,在Rt△ABC的斜边BC上截取CD= CA,过点D作DE⊥BC交AB于E,则有( )


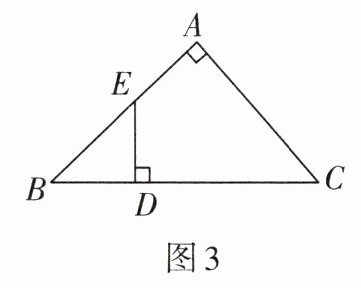
A.DE= DB

B.DE= AE
C.AE= BE
D.AE= BD

答案： B

1. 如图4,AB= AD,AD⊥DC,BC⊥AB,AC和BD相交于点E,则Rt△ABC≌Rt△______,依据是______；进而可推出△CDE≌△______,依据是______.

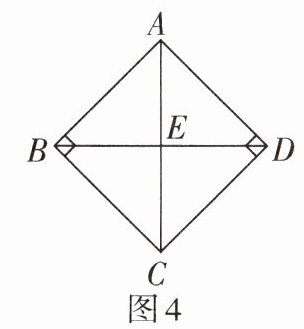
答案： ADC, HL, CBE, SAS

2. 如图5,∠C= ∠C'= 90°,欲判定△ABC≌△A'B'C',可添加条件AC= A'C'和______(添上一个条件即可).

答案： AB=A'B'(或 BC=B'C'或∠A=∠A'或∠B=∠B')

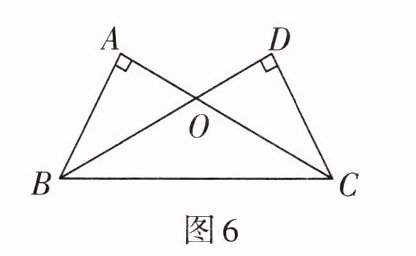
3. 如图6,∠A= ∠D= 90°,AC= DB,欲证OB= OC,可以先利用“HL”证明______≌______得到AB= DC；再利用“______”证明△AOB≌______,从而得到OB= OC.

答案： Rt△ABC, Rt△DCB, AAS, △DOC

4. 如图7,在Rt△ABC中,∠C= 90°,AC= 15 cm,BC= 8 cm,AX⊥AC于点A,P,Q两点分别在边AC和射线AX上移动,且PQ= AB,当AP= ______cm时,△ABC和△APQ全等.

答案： 8或15