《2025年新课程课堂同步练习册八年级数学上册人教版》

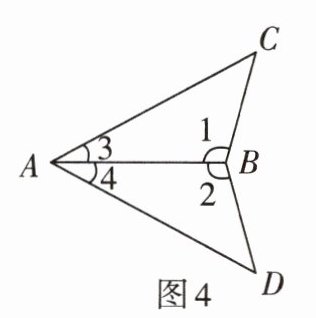
2. 如图4,$\angle 1= \angle 2$。
(1)当$BC= BD$时,判定$\triangle ABC\cong\triangle ABD$的依据是______；
(2)当$\angle 3= \angle 4$时,判定$\triangle ABC\cong\triangle ABD$的依据是______。

答案：
(1)SAS
(2)ASA

3. 已知在$\triangle ABC和\triangle A_{1}B_{1}C_{1}$中,$AB= A_{1}B_{1}$,$\angle A= \angle A_{1}$,要使$\triangle ABC\cong\triangle A_{1}B_{1}C_{1}$,还需要添加一个条件,这个条件可以是______。

答案： (答案不唯一)$∠B=∠B_{1}$或$∠C=∠C_{1}$或$AC=A_{1}C_{1}$

4. 如图5,甲、乙、丙三个三角形中和$\triangle ABC$全等的图形是______。

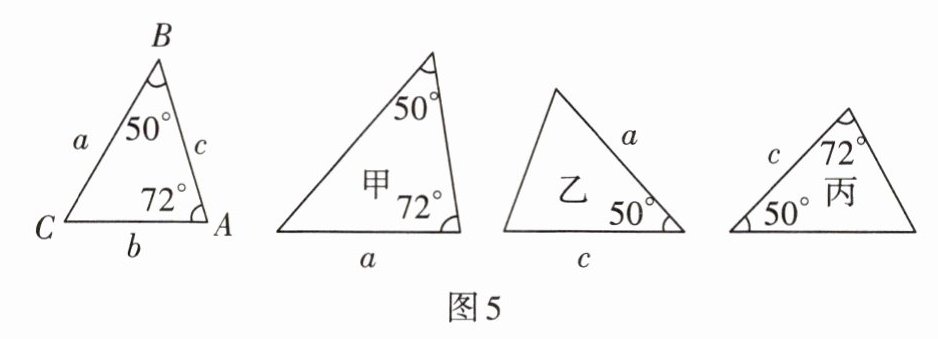
答案： 乙、丙

5. 如图6,$AC与BD交于点O$,$AB// DC$,补充一个条件______,可推出$\triangle AOB\cong\triangle COD$。

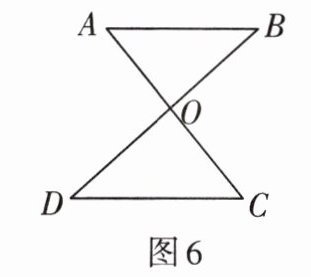
答案： $AB=CD$或$OA=OC$或$OB=OD$

1. 如图7,$BD= CE$,$\angle B= \angle C$。
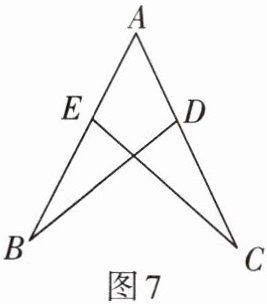
求证：$\triangle ACE\cong\triangle ABD$。

答案： 在$\triangle ACE$和$\triangle ABD$中，
$\begin{matrix}\angle A=\angle A(公共角),\\ \angle B=\angle C(已知),\\BD=CE(已知).\end{matrix}$
根据$AAS$（角角边）判定定理：
$\triangle ACE\cong\triangle ABD(AAS)$。

2. 如图8,点$B$,$E$,$C$,$F$在同一直线上,$AB// DE$,$AC// DF$,$BE= CF$。
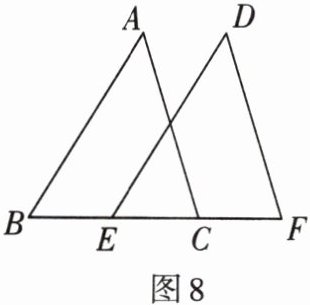
求证：$AB= DE$。

答案： 提示:证$△ABC\cong △DEF(ASA)$.