《2025年新课程课堂同步练习册八年级数学上册人教版》

3. 已知一个长方形的周长为$80cm$,面积为$36cm^2$,试问以该长方形的长和宽为边长的两个正方形的面积之和是多少？

答案： $1528\,cm^{2}$

4. 某镇正在建造的文化广场工地上,有两种铺设广场地面的材料,一种是长为$a$,宽为$b$的长方形板材(如图1),另一种是边长为$c$的正方形地砖(如图2).

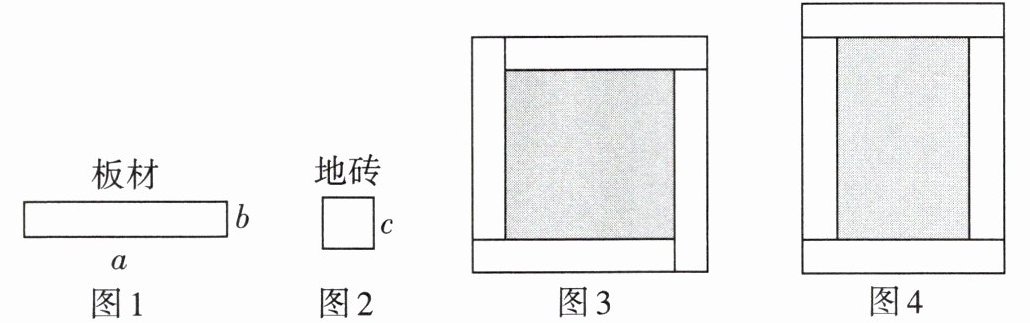
(1) 用几块如图2所示的正方形地砖能拼出一个新的正方形？并写出新正方形的面积(写出一个符合条件的答案即可).
(2) 用如图1所示的四块长方形板材铺成如图3的大正方形或如图4的大长方形,中间分别空出一个小正方形和小长方形(即图中阴影部分).
① 请用含$a$、$b$的代数式分别表示图3和图4中阴影部分的面积.
② 图3和图4中阴影部分的面积哪个大？大多少？

答案：
(1)四块即可拼成一个边长的$2c$的正方形,则面积是$4c^{2}$.（答案不唯一）
(2)①图3中阴影部分的面积是：$(a-b)^{2}$,图4中阴影部分的面积是：$a(a-2b)$ ②$\because(a-b)^{2}-a(a-2b)=a^{2}-2ab+b^{2}-a^{2}+2ab=b^{2}＞0$,$\therefore(a-b)^{2}＞a(a-2b)$.故图3中阴影部分的面积较大,大$b^{2}$