《2025年资源与评价黑龙江教育出版社八年级数学上册人教版》

6. 如图,BP,CP分别是△ABC的外角∠CBD,∠ECB的平分线。小明经过分析后,得出了以下结论：①点P在∠BAC的平分线上；②BP= CP；③点P到AD,AE,BC的距离相等。把你认为正确的结论的序号写在横线上：①③。

答案： ①③

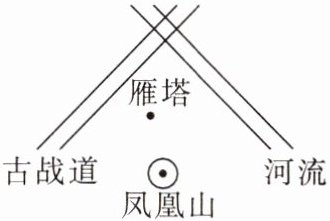
7. 某考古队为进行考古研究,寻找一座古城遗迹,根据史料记载,这座古城在古战道与河流之间且到古战道与河流距离相等,在凤凰山附近且距离雁塔200 m的位置,考古队员很快找到了这座古城的遗址,你能用学过的知识在图中合理标出古城遗址吗？(比例尺为1:10 000)

答案：
解：如图，设古战道与河流交于点 O，OA 表示河流，OB 表示古战道，点 C 表示雁塔，点 D 表示凤凰山. 用直尺和圆规作出∠AOB 的平分线 OP. 以点 C 为圆心，2 cm 长为半径作圆交 OP 于点 M，点 M 即为古城遗址.

8. 如图,在Rt△ABC中,∠ACB= 90°,BD是△ABC的一条角平分线。O是BD上的一点,过点O分别作AC,BC的垂线,垂足分别为F,E,连接OC,OA,若∠FCO= 45°,求证：点O在∠BAC的平分线上。

答案：
证明：如图，过点 O 作 OH⊥AB 于点 H，
∵BD 是△ABC 的一条角平分线，OE⊥BC，OH⊥AB，
∴OE=OH.
∵∠ACB=90°，∠FCO=45°，
∴CO 平分∠ACB.
∵OE⊥BC，OF⊥AC，
∴OE=OF，
∴OF=OH，
∴点 O 在∠BAC 的平分线上.

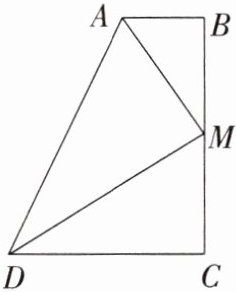
9. 如图,∠B= ∠C= 90°,M是BC的中点,且DM平分∠ADC。
(1)求证：AM平分∠DAB。
(2)试说明线段DM与AM有怎样的位置关系,并证明你的结论。

答案：

(1)证明：如图，过点 M 作 ME⊥AD 于点 E.
∵DM 平分∠ADC，∠C=90°，ME⊥AD，
∴MC=ME.
∵M 为 BC 的中点，
∴BM=MC=ME.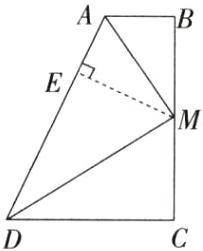
∵∠B=90°，ME⊥AD，
∴AM 平分∠DAB.
(2)AM⊥DM.证明：
∵AB//DC，
∴∠BAD+∠ADC=180°.
∵AM 平分∠DAB，DM 平分∠ADC，
∴∠MAD=$\frac{1}{2}$∠BAD，∠MDA=$\frac{1}{2}$∠ADC，
∴∠MAD+∠MDA=90°，
∴∠AMD=90°，
∴AM⊥DM.