第3页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
1. 下面是小强用三根火柴组成的图形,其中符合三角形概念的是(

C
)
答案:
C
2. 如图,以 BC 为边的三角形有(

A.1 个
B.2 个
C.3 个
D.4 个
C
)
A.1 个
B.2 个
C.3 个
D.4 个
答案:
C
3. 如图,在△ABD 中,∠A 的对边是(
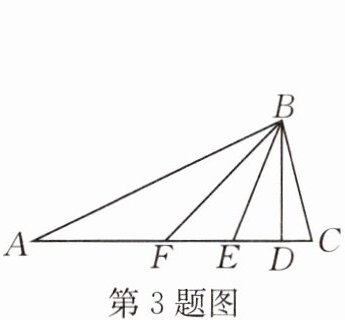
A.BF
B.BE
C.BD
D.BC
C
)
A.BF
B.BE
C.BD
D.BC
答案:
C
4. 如图,以点 A 为顶点的三角形有(
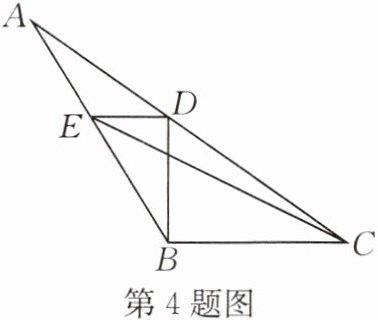
A.4 个
B.3 个
C.2 个
D.1 个
A
)
A.4 个
B.3 个
C.2 个
D.1 个
答案:
A
5. 图中三角形的个数是(

A.4
B.5
C.6
D.7
B
)
A.4
B.5
C.6
D.7
答案:
B
6. 若有一条公共边的两个三角形称为一对“共边三角形”,则图中以 BC 为公共边的“共边三角形”有(
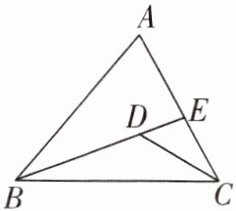
A.2 对
B.3 对
C.4 对
D.6 对
B
)
A.2 对
B.3 对
C.4 对
D.6 对
答案:
B
7. 如图,这是一个由几个小三角形拼成的大三角形,则该图中三角形的个数有(
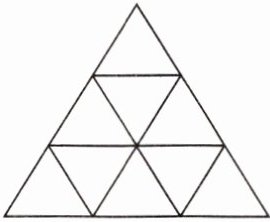
A.10 个
B.12 个
C.13 个
D.15 个
C
)
A.10 个
B.12 个
C.13 个
D.15 个
答案:
C
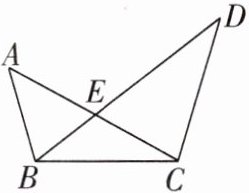
8. 观察下图,并回答下列问题。
(1)图中有几个三角形?用符号表示这些三角形。
(2)以 AB 为边的三角形有哪些?
(3)以 E 为顶点的三角形有哪些?
(4)以∠D 为角的三角形有哪些?
(1)图中有几个三角形?用符号表示这些三角形。
(2)以 AB 为边的三角形有哪些?
(3)以 E 为顶点的三角形有哪些?
(4)以∠D 为角的三角形有哪些?

答案:
解:
(1)5个,△ABE,△BCE,△CDE,△ABC,△BCD.
(2)△ABC,△ABE.
(3)△ABE,△BCE,△CDE.
(4)△BCD,△DEC.
(1)5个,△ABE,△BCE,△CDE,△ABC,△BCD.
(2)△ABC,△ABE.
(3)△ABE,△BCE,△CDE.
(4)△BCD,△DEC.
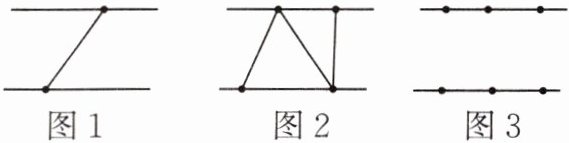
9. 两条平行直线上各有 n 个点,用这 n 对点按如下的规则连接线段:
①平行线之间的点在连线段时,可以有共同的端点,但不能有其他交点;
②符合①要求的线段必须全部画出。
图 1 展示了当 n = 1 时的情况,此时图中三角形的个数为 0;
图 2 展示了当 n = 2 时的一种情况,此时图中三角形的个数为 2。
(1)当 n = 3 时,请在图 3 中画出使三角形个数最少的图形,此时图中三角形的个数为______。
(2)试猜想当 n 对点时,按上述规则画出的图形中,最少有多少个三角形?
(3)当 n = 2025 时,按上述规则画出的图形中,最少有多少个三角形?
①平行线之间的点在连线段时,可以有共同的端点,但不能有其他交点;
②符合①要求的线段必须全部画出。
图 1 展示了当 n = 1 时的情况,此时图中三角形的个数为 0;
图 2 展示了当 n = 2 时的一种情况,此时图中三角形的个数为 2。
(1)当 n = 3 时,请在图 3 中画出使三角形个数最少的图形,此时图中三角形的个数为______。
(2)试猜想当 n 对点时,按上述规则画出的图形中,最少有多少个三角形?
(3)当 n = 2025 时,按上述规则画出的图形中,最少有多少个三角形?

答案:
解:
(1)如图(画法不唯一),最少有4个三角形.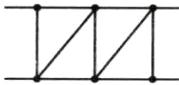
(2)当有n对点时,最少可以画2(n-1)个三角形.
(3)2×(2025-1)=4048(个).答:当n=2025时,最少可以画4048个三角形.
解:
(1)如图(画法不唯一),最少有4个三角形.

(2)当有n对点时,最少可以画2(n-1)个三角形.
(3)2×(2025-1)=4048(个).答:当n=2025时,最少可以画4048个三角形.
查看更多完整答案,请扫码查看


